Dans ce travail, on étudie les propriétés de la conorme, c(a) d'un élément a d'une C*-algèbre A. Nous montrons que c(a) est aussi douée de la condition de B*- algèbre, c'est-à-dire qu'elle vérifie l'égalité: c(a)2 = c(a*a) = c(aa*) = c(a*)2. Nous remarquons que la conorme est invariante par restriction à toute sous-C*-algèbre de A, propriété connue pour le spectre.
Soit {an} une suite d'éléments réguliers telle que an → a régulier. Nous donnons des conditions nécessaires et suffisantes pour que 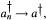 où a† désigne l'inverse de Moore-Penrose de a.
où a† désigne l'inverse de Moore-Penrose de a.

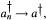 où a
où a