6 results
ON A DIRICHLET PROBLEM WITH p-LAPLACIAN AND SET-VALUED NONLINEARITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 14 October 2011, pp. 83-89
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
On the Solvability of a Neumann Boundary Value Problem at Resonance
-
- Journal:
- Canadian Mathematical Bulletin / Volume 40 / Issue 4 / 01 December 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 464-470
- Print publication:
- 01 December 1997
-
- Article
-
- You have access
- Export citation
A Local Hopf Bifurcation Theorem for a Certain Class of Implicit Differential Equations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 36 / Issue 2 / 01 June 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 183-189
- Print publication:
- 01 June 1993
-
- Article
-
- You have access
- Export citation
Points of Spherical Maxima and Solvability of Semilinear Elliptic Equations
-
- Journal:
- Canadian Journal of Mathematics / Volume 43 / Issue 4 / 01 August 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 825-831
- Print publication:
- 01 August 1991
-
- Article
-
- You have access
- Export citation
A Note on Locally Expansive and Locally Accretive Operators
-
- Journal:
- Canadian Mathematical Bulletin / Volume 26 / Issue 2 / 01 June 1983
- Published online by Cambridge University Press:
- 20 November 2018, pp. 228-232
- Print publication:
- 01 June 1983
-
- Article
-
- You have access
- Export citation
On the Solvability and Continuation Type Results for Nonlinear Equations with Applications, II
-
- Journal:
- Canadian Mathematical Bulletin / Volume 25 / Issue 1 / 01 March 1982
- Published online by Cambridge University Press:
- 20 November 2018, pp. 98-109
- Print publication:
- 01 March 1982
-
- Article
-
- You have access
- Export citation

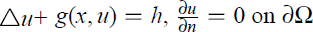 in which the non-linearity
in which the non-linearity 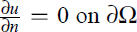 in which the nonlinear term g may grow superlinearly in
in which the nonlinear term g may grow superlinearly in 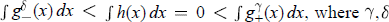 are arbitrarily nonnegative constants,
are arbitrarily nonnegative constants, 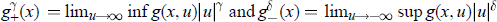 . The proofs are based upon degree theoretic arguments.
. The proofs are based upon degree theoretic arguments.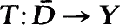 closed, locally
closed, locally 