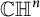 $\mathbb {CH} ^{n}$
$\mathbb {CH} ^{n}$
 $\mathbb {C}$-FUCHSIAN SUBGROUPS OF SOME NONARITHMETIC LATTICES
$\mathbb {C}$-FUCHSIAN SUBGROUPS OF SOME NONARITHMETIC LATTICES
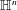 $\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
$\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups