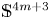 $\mathbb {S}^{4m+3}$ as the principal orbit
$\mathbb {S}^{4m+3}$ as the principal orbit
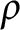 $\rho $
-Einstein solitons on Sasakian manifolds
$\rho $
-Einstein solitons on Sasakian manifolds