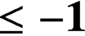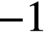4 results
Anisotropic Gauss curvature flows and their associated Dual Orlicz-Minkowski problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 01 November 2021, pp. 148-162
- Print publication:
- February 2022
-
- Article
- Export citation
REALIZING METRICS OF CURVATURE
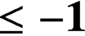 $\mathbf {\leq -1}$
ON CLOSED SURFACES IN FUCHSIAN ANTI-DE SITTER MANIFOLDS
$\mathbf {\leq -1}$
ON CLOSED SURFACES IN FUCHSIAN ANTI-DE SITTER MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 19 February 2021, pp. 312-334
- Print publication:
- June 2022
-
- Article
- Export citation
Separation of variables in equations of mean-curvature type
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1017-1035
- Print publication:
- October 2016
-
- Article
- Export citation
OPTIMAL SMOOTHING FOR CONVEX POLYTOPES
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 36 / Issue 4 / July 2004
- Published online by Cambridge University Press:
- 14 June 2004, pp. 483-492
- Print publication:
- July 2004
-
- Article
- Export citation