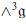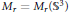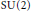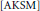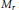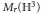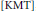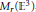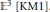4 results
Central Extensions of Loop Groups and Obstruction to Pre-Quantization
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 1 / 01 March 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 116-126
- Print publication:
- 01 March 2013
-
- Article
-
- You have access
- Export citation
Sur la structure transverse à une orbite nilpotente adjointe
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 4 / 01 August 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 750-770
- Print publication:
- 01 August 2005
-
- Article
-
- You have access
- Export citation
Quasi-Poisson Manifolds
-
- Journal:
- Canadian Journal of Mathematics / Volume 54 / Issue 1 / 01 February 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-29
- Print publication:
- 01 February 2002
-
- Article
-
- You have access
- Export citation
The Symplectic Geometry of Polygons in the 3-Sphere
-
- Journal:
- Canadian Journal of Mathematics / Volume 54 / Issue 1 / 01 February 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 30-54
- Print publication:
- 01 February 2002
-
- Article
-
- You have access
- Export citation