We compute $ku^*\left(K\!\left({\mathbb{Z}}_p,2\right)\right)$ and $ku_*\left(K\!\left({\mathbb{Z}}_p,2\right)\right)$, the connective $KU$-cohomology and connective $KU$-homology groups of the mod-$p$ Eilenberg–MacLane space $K\!\left({\mathbb{Z}}_p,2\right)$, using the Adams spectral sequence. We obtain a striking interaction between $h_0$-extensions and exotic extensions. The mod-$p$ connective $KU$-cohomology groups, computed elsewhere, are needed in order to establish higher differentials and exotic extensions in the integral groups.

We prove the convergence of the Adams spectral sequence based on Morava K-theory and relate it to the filtration by powers of the maximal ideal in the Lubin–Tate ring through a Miller square. We use the filtration by powers to construct a spectral sequence relating the homology of the K-local sphere to derived functors of completion and express the latter as cohomology of the Morava stabiliser group. As an application, we compute the zeroth limit at all primes and heights.

We show that the Gromov-Lawson-Rosenberg conjecture for the Semi-Dihedral group of order 16 is true.

We present a new proof of Anderson's result that the real K-theory spectrum is Anderson self-dual up to a fourfold suspension shift; more strongly, we show that the Anderson dual of the complex K-theory spectrum KU is C2-equivariantly equivalent to Σ4KU, where C2 acts by complex conjugation. We give an algebro-geometric interpretation of this result in spectrally derived algebraic geometry and apply the result to calculate 2-primary Gross-Hopkins duality at height 1. From the latter we obtain a new computation of the group of exotic elements of the K(1)-local Picard group.

For a compact simply connected simple Lie group G with an involution α, we compute the G ⋊ ℤ/2-equivariant K-theory of G where G acts by conjugation and ℤ/2 acts either by α or by g ↦ α(g)−1. We also give a representation-theoretic interpretation of those groups, as well as of KG(G).

We make explicit Poincaré duality for the equivariant K-theory of equivariant complex projective spaces. The case of the trivial group provides a new approach to the K-theory orientation [3].

Let $\Cal F$ be a holomorphic foliation (possibly with singularities) on a non-singular manifold $M$, and let $V$ be a complex analytic subset of $M$. Usual residue theorems along $V$ in the theory of complex foliations require that $V$ be tangent to the foliation (that is, a union of leaves and singular points of $V$ and $\Cal F$); this is the case for instance for the blow-up of a non-dicritical isolated singularity. In this paper, residue theorems are introduced along subvarieties that are not necessarily tangent to the foliation, including the blow-up of the dicritical situation.

In the first paper with the same title the authors were able to determine all partially oriented flag manifolds that are stably parallelizable or parallelizable, apart from four infinite families that were undecided. Here, using more delicate techniques (mainly K-theory),we settle these previously undecided families and show that none of the manifolds in them is stably parallelizable, apart from one 30-dimensional manifold which still remains undecided.

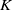
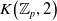
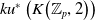
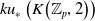
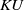
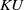
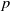
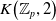
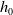
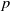
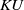
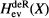In [Con2] Connes introduced cyclic cohomology HC*(A) for an associative algebra A. When A is a complex algebra he constructed a Chern character for p-summable Fredholm modules over A taking values in HC*(A). As a very special case, when X is a closed C∞-manifold and A = C∞ (X), this construction recovers the usual Chern character, which is a rational isomorphism from the K-homology K0(X) to , the even dimensional deRham homology of X.

In this paper we give a description of:

(1) the Hopf algebra structure of k*(G; L) when G is a compact, connected Lie group and L is a ring of type Q(P) so that H*(G; L) is torsion free;

(2) the algebra structure of k*(G2; L) for L = Z2 or Z.

The fact that no real Grassmann manifolds Gk(Rn) are parallelizable (or even stably parallelizable) except for the obvious cases G1R2≅S1, G1(R4)≅G3(R4) ≅ RP3, and G1(R8)≅ G7(R8) ≅ RP7 was first noted by Hiller and Stong. Their work in turn depends on induction and the work of Oproiu, who examined detailed calculations of Stiefel-Whitney classes for k = 2, 3. In this note we give a short proof of this result, using elementary results from K-theory, that also covers the complex and quaternionic Grassmann manifolds.