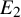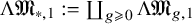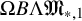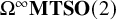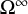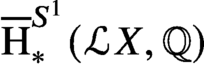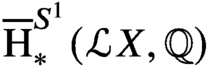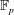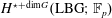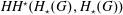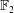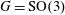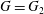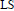5 results
Parametrised moduli spaces of surfaces as infinite loop spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hodge decomposition of string topology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 13 April 2021, e33
-
- Article
-
- You have access
- Open access
- Export citation
Koszul A∞-algebras and free loop space homology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 37-65
-
- Article
- Export citation
The Batalin–Vilkovisky Algebra in the String Topology of Classifying Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 843-889
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Lusternik-Schnirelmann Category and Algebraic R-Local Homotopy Theory
-
- Journal:
- Canadian Journal of Mathematics / Volume 50 / Issue 4 / 01 August 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 845-862
- Print publication:
- 01 August 1998
-
- Article
-
- You have access
- Export citation