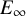 $E_{\infty }$-coalgebra model of the based loop space
$E_{\infty }$-coalgebra model of the based loop space
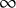 $\infty $
-groupoid objects
$\infty $
-groupoid objects