7 results
Transversality theorem in o-minimal structures
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1227-1234
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
THE HOROSPHERICAL GEOMETRY OF SUBMANIFOLDS IN HYPERBOLIC SPACE
-
- Journal:
- Journal of the London Mathematical Society / Volume 71 / Issue 3 / June 2005
- Published online by Cambridge University Press:
- 24 May 2005, pp. 779-800
- Print publication:
- June 2005
-
- Article
- Export citation
INFINITE RELATIVE DETERMINACY OF SMOOTH FUNCTION GERMS WITH TRANSVERSE ISOLATED SINGULARITIES AND RELATIVE ŁOJASIEWICZ CONDITIONS
-
- Journal:
- Journal of the London Mathematical Society / Volume 69 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 29 March 2004, pp. 518-530
- Print publication:
- April 2004
-
- Article
- Export citation
The Stability Theorems for Subgroups of
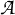 and
and 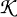
-
- Journal:
- Canadian Journal of Mathematics / Volume 46 / Issue 5 / 01 October 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 995-1006
- Print publication:
- 01 October 1994
-
- Article
-
- You have access
- Export citation
Blow Analytic Mappings and Functions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 36 / Issue 4 / 01 December 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 497-506
- Print publication:
- 01 December 1993
-
- Article
-
- You have access
- Export citation
On the Stability of Equivariant Bifurcation Problems and Their Unfoldings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 35 / Issue 2 / 01 June 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 237-246
- Print publication:
- 01 June 1992
-
- Article
-
- You have access
- Export citation
Topological Properties of Legendrian Singularities
-
- Journal:
- Canadian Mathematical Bulletin / Volume 34 / Issue 3 / 01 September 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 357-363
- Print publication:
- 01 September 1991
-
- Article
-
- You have access
- Export citation

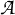 and
and 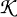
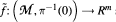 such that
such that 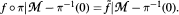 Then an inverse mapping theorem for blow analytic mappings as a generalization of classical theorem is shown. And the following is shown. Theorem: The analytic family of blow analytic functions with isolated singularities admits an analytic trivialization after blowing-up.
Then an inverse mapping theorem for blow analytic mappings as a generalization of classical theorem is shown. And the following is shown. Theorem: The analytic family of blow analytic functions with isolated singularities admits an analytic trivialization after blowing-up.