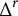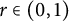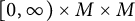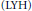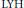6 results
Heat kernel asymptotics for real powers of Laplacians
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 January 2023, pp. 367-393
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Second-order differential equations with random perturbations and small parameters
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 05 July 2017, pp. 763-779
- Print publication:
- August 2017
-
- Article
- Export citation
Thin Layer Models for Electromagnetism
-
- Journal:
- Communications in Computational Physics / Volume 16 / Issue 1 / July 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 213-238
- Print publication:
- July 2014
-
- Article
- Export citation
Pseudolocality for the Ricci Flow and Applications
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 1 / 01 February 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 55-85
- Print publication:
- 01 February 2011
-
- Article
-
- You have access
- Export citation
REGULARIZED TRACES AND TAYLOR EXPANSIONS FOR THE HEAT SEMIGROUP
-
- Journal:
- Journal of the London Mathematical Society / Volume 68 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 25 September 2003, pp. 402-418
- Print publication:
- October 2003
-
- Article
- Export citation
Morse inequalities for covering manifolds
-
- Journal:
- Nagoya Mathematical Journal / Volume 163 / September 2001
- Published online by Cambridge University Press:
- 22 January 2016, pp. 145-165
- Print publication:
- September 2001
-
- Article
-
- You have access
- Export citation