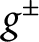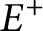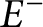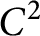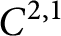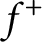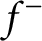12 results
Exponential ergodicity and steady-state approximations for a class of markov processes under fast regime switching
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 March 2021, pp. 1-29
- Print publication:
- March 2021
-
- Article
- Export citation
Optimal free export/import regions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 17 September 2020, pp. 737-751
- Print publication:
- December 2021
-
- Article
- Export citation
A non-local traffic flow model for 1-to-1 junctions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 16 December 2019, pp. 1029-1049
-
- Article
- Export citation
Traffic flow densities in large transport networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 17 November 2017, pp. 1091-1115
- Print publication:
- December 2017
-
- Article
- Export citation
Lattice Free Stochastic Dynamics
-
- Journal:
- Communications in Computational Physics / Volume 12 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 691-702
- Print publication:
- September 2012
-
- Article
- Export citation
Transient Moments of the TCP Window Size Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 163-175
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Uniform renewal theory with applications to expansions of random geometric sums
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1070-1097
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
A Stochastic Ordering Property for Leaky Bucket Regulated Flows in Packet Networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 332-348
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
NONCONVEX CONSERVATION LAWS AND ORDINARY DIFFERENTIAL EQUATIONS
-
- Journal:
- Journal of the London Mathematical Society / Volume 69 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 29 March 2004, pp. 428-440
- Print publication:
- April 2004
-
- Article
- Export citation
Estimating tail decay for stationary sequences via extreme values
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 198-226
- Print publication:
- March 2004
-
- Article
- Export citation
Poisson traffic flow in a general feedback queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 3 / September 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 630-636
- Print publication:
- September 2002
-
- Article
- Export citation
Servers in tandem with k-stage blocking and communications-type flow
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1061-1069
- Print publication:
- December 1994
-
- Article
- Export citation