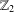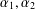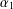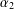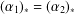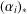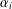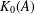3 results
A REMARK ON THE TRACIAL ROKHLIN PROPERTY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 07 March 2018, pp. 492-498
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
The Category of Bratteli Diagrams
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 5 / 01 October 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 990-1023
- Print publication:
- 01 October 2015
-
- Article
-
- You have access
- Export citation
Berg's Technique for Pseudo-Actions With Applications to af Embeddings
-
- Journal:
- Canadian Journal of Mathematics / Volume 43 / Issue 1 / 01 February 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 119-157
- Print publication:
- 01 February 1991
-
- Article
-
- You have access
- Export citation