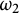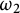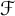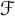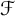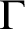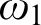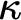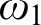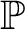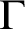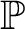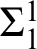We prove that it is consistent that Club Stationary Reflection and the Special Aronszajn Tree Property simultaneously hold on
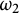 $\omega _2$
, thereby contributing to the study of the tension between compactness and incompactness in set theory. The poset which produces the final model follows the collapse of an ineffable cardinal first with an iteration of club adding (with anticipation) and second with an iteration specializing Aronszajn trees.
$\omega _2$
, thereby contributing to the study of the tension between compactness and incompactness in set theory. The poset which produces the final model follows the collapse of an ineffable cardinal first with an iteration of club adding (with anticipation) and second with an iteration specializing Aronszajn trees.
In the first part of the paper, we prove a general theorem about specializing Aronszajn trees on
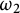 $\omega _2$
after forcing with what we call
$\omega _2$
after forcing with what we call
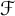 $\mathcal {F}$
-Strongly Proper posets, where
$\mathcal {F}$
-Strongly Proper posets, where
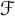 $\mathcal {F}$
is either the weakly compact filter or the filter dual to the ineffability ideal. This type of poset, of which the Levy collapse is a degenerate example, uses systems of exact residue functions to create many strongly generic conditions. We prove a new result about stationary set preservation by quotients of this kind of poset; as a corollary, we show that the original Laver–Shelah model, which starts from a weakly compact cardinal, satisfies a strong stationary reflection principle, although it fails to satisfy the full Club Stationary Reflection. In the second part, we show that the composition of collapsing and club adding (with anticipation) is an
$\mathcal {F}$
is either the weakly compact filter or the filter dual to the ineffability ideal. This type of poset, of which the Levy collapse is a degenerate example, uses systems of exact residue functions to create many strongly generic conditions. We prove a new result about stationary set preservation by quotients of this kind of poset; as a corollary, we show that the original Laver–Shelah model, which starts from a weakly compact cardinal, satisfies a strong stationary reflection principle, although it fails to satisfy the full Club Stationary Reflection. In the second part, we show that the composition of collapsing and club adding (with anticipation) is an
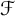 $\mathcal {F}$
-Strongly Proper poset. After proving a new result about Aronszajn tree preservation, we show how to obtain the final model.
$\mathcal {F}$
-Strongly Proper poset. After proving a new result about Aronszajn tree preservation, we show how to obtain the final model.