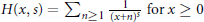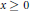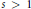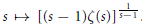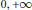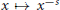1 results
Convexité, complête monotonie et inégalités sur les fonctions zêta et gamma, sur les fonctions des opérateurs de Baskakov et sur des fonctions arithmétiques
-
- Journal:
- Canadian Journal of Mathematics / Volume 54 / Issue 5 / 01 October 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 916-944
- Print publication:
- 01 October 2002
-
- Article
-
- You have access
- Export citation
-
Nous prouvons un encadrement optimal pour la quantité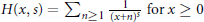
$H\left( x,\,s \right)\,=\,\sum{_{n\ge 1}\,\frac{1}{{{\left( x+n \right)}^{s}}}}$ pour 
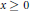$x\,\ge \,0$ et 
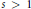$s\,>\,1$, qui améliore l'encadrement standard par des intégrales. Cet encadrement entraîne des inégalités sur la fonction 
$\zeta $ de Riemann, et amène à conjecturer la monotonie de la fonction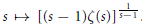 
$s\,\mapsto \,{{[(s\,-\,1)\text{ }\!\!\zeta\!\!\text{ (}s\text{)}]}^{\frac{1}{S-1}}}$. On donne des applications à l'étude de la convexité de fonctions liées à la fonction 
$\Gamma $ d'Euler et à la majoration optimale des fonctions élémentaires intervenant dans les opérateurs de Baskakov. Puis, nous étendons aux fonctions complètement monotones sur ]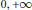
$0,\,+\infty $[ les résultats établis pour la fonction 
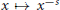$x\,\mapsto \,{{x}^{-s}}$, et nous en déduisons des preuves élémentaires du comportement, quand 
$z$ tend vers 1, des séries génératrices de certaines fonctions arithmétiques. Enfin, nous prouvons qu'une partie du résultat se généralise à une classe de fonctions convexes positives décroissantes.
