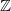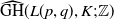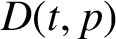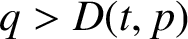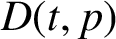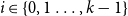Refine search
Actions for selected content:
18 results
Wine Stars & Bars: The combinatorics of critic consensus and the usefulness of order preference models
-
- Journal:
- Journal of Wine Economics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An update on the coin-moving game on the square grid
-
-
- Book:
- Games of No Chance 6
- Published online:
- 18 May 2025
- Print publication:
- 05 June 2025, pp 369-404
-
- Chapter
- Export citation
3 - Geometric Rigidity Theory
- from Part I - Maxwell and Structural Mechanics
-
-
- Book:
- The Geometry of Equilibrium
- Published online:
- 03 May 2025
- Print publication:
- 22 May 2025, pp 29-44
-
- Chapter
- Export citation
A NOTE ON THE STRONG ERDŐS–HAJNAL PROPERTY FOR GRAPHS WITH BOUNDED VC-MINIMAL COMPLEXITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 November 2024, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMBINATORIAL BOUNDS IN DISTAL STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 13 October 2023, pp. 1-33
-
- Article
- Export citation
A note on grid homology in lens spaces:
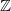 $\mathbb{Z}$ coefficients and computations
$\mathbb{Z}$ coefficients and computations
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 31 March 2023, pp. 457-479
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
5 - Probability Theory
-
- Book:
- The Failures of Mathematical Anti-Evolutionism
- Published online:
- 28 April 2022
- Print publication:
- 12 May 2022, pp 110-162
-
- Chapter
- Export citation
SUBSHIFTS OF FINITE TYPE WITH A HOLE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 22 March 2022, pp. 73-98
- Print publication:
- August 2023
-
- Article
- Export citation
A blurred view of Van der Waerden type theorems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 26 November 2021, pp. 684-701
-
- Article
- Export citation
5 - Combinatorics of Orthogonal Polynomials and their Moments
-
-
- Book:
- Lectures on Orthogonal Polynomials and Special Functions
- Published online:
- 07 October 2020
- Print publication:
- 15 October 2020, pp 280-334
-
- Chapter
- Export citation
5 - Flat Vertex Folds: Local Properties
- from Part II - The Combinatorial Geometry of Flat Origami
-
- Book:
- Origametry
- Published online:
- 06 October 2020
- Print publication:
- 08 October 2020, pp 75-106
-
- Chapter
- Export citation
7 - Counting Flat Folds
- from Part II - The Combinatorial Geometry of Flat Origami
-
- Book:
- Origametry
- Published online:
- 06 October 2020
- Print publication:
- 08 October 2020, pp 137-158
-
- Chapter
- Export citation

Origametry
- Mathematical Methods in Paper Folding
-
- Published online:
- 06 October 2020
- Print publication:
- 08 October 2020

Surveys in Combinatorics 2019
-
- Published online:
- 17 June 2019
- Print publication:
- 27 June 2019
Semidefinite Programming BasedAlgorithms for the Sparsest Cut Problem
-
- Journal:
- RAIRO - Operations Research / Volume 45 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 17 June 2011, pp. 75-100
- Print publication:
- April 2011
-
- Article
- Export citation
ON A COMBINATORIAL PROOF FOR AN IDENTITY INVOLVING THE TRIANGULAR NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 27 September 2010, pp. 46-49
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
Duration of a secretary problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 556-558
- Print publication:
- June 1997
-
- Article
- Export citation