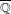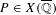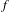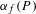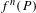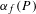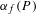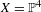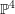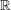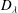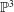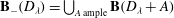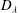6 results
Galois points and Cremona transformations
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 471-478
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A rational map with infinitely many points of distinct arithmetic degrees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 12 April 2019, pp. 3051-3055
- Print publication:
- November 2020
-
- Article
- Export citation
Cremona transformations and derived equivalences of K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 28 May 2018, pp. 1508-1533
- Print publication:
- July 2018
-
- Article
-
- You have access
- HTML
- Export citation
The diminished base locus is not always closed
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 10 / October 2014
- Published online by Cambridge University Press:
- 15 September 2014, pp. 1729-1741
- Print publication:
- October 2014
-
- Article
- Export citation
Geometrically rational real conic bundles and very transitive actions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 13 September 2010, pp. 161-187
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
On Birational Maps and Jacobian Matrices
-
- Journal:
- Compositio Mathematica / Volume 126 / Issue 3 / May 2001
- Published online by Cambridge University Press:
- 04 December 2007, pp. 335-358
- Print publication:
- May 2001
-
- Article
-
- You have access
- Export citation

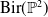
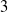
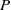
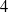
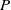
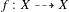 be a dominant rational self-map of a smooth projective variety defined over
be a dominant rational self-map of a smooth projective variety defined over