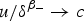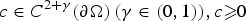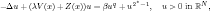Refine search
Actions for selected content:
9 results
Positive solutions of semilinear elliptic problems with a Hardy potential
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 15 February 2019, pp. 1791-1804
- Print publication:
- August 2020
-
- Article
- Export citation
An Extrapolation Cascadic Multigrid Method for Elliptic Problems on Reentrant Domains
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1347-1363
- Print publication:
- December 2017
-
- Article
- Export citation
A posteriori error estimates for ellipticproblems with Dirac measure terms in weighted spaces
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 6 / November 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 1557-1581
- Print publication:
- November 2014
-
- Article
- Export citation
Analysis of Compatible Discrete Operator schemes for elliptic problems on polyhedral meshes
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 2 / March 2014
- Published online by Cambridge University Press:
- 20 January 2014, pp. 553-581
- Print publication:
- March 2014
-
- Article
- Export citation
INHOMOGENEOUS PERIODIC PARABOLIC PROBLEMS WITH INDEFINITE DATA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 06 September 2011, pp. 516-524
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Solvability conditions for some non-Fredholm operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 30 November 2010, pp. 249-271
-
- Article
-
- You have access
- Export citation
Multiplicity of positive solutions for a class of problems with critical growth in ℝN
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 1-21
-
- Article
-
- You have access
- Export citation
A Posteriori Error Estimates for Finite Volume Approximations
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 4 / Issue 1 / 2009
- Published online by Cambridge University Press:
- 27 January 2009, pp. 106-122
- Print publication:
- 2009
-
- Article
- Export citation
Numerical computation of solitons for optical systems
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 43 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 05 December 2008, pp. 173-208
- Print publication:
- January 2009
-
- Article
- Export citation