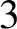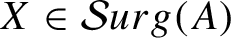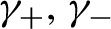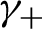1 results
Anosov flows on
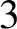 $3$
-manifolds: the surgeries and the foliations
$3$
-manifolds: the surgeries and the foliations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 27 April 2022, pp. 1129-1188
- Print publication:
- April 2023
-
- Article
- Export citation