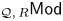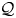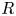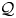1 results
Flat model structures and Gorenstein objects in functor categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation
-
We construct a flat model structure on the category ${_{\mathcal {Q},\,R}\mathsf {Mod}}$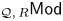
of additive functors from a small preadditive category $\mathcal {Q}$
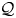satisfying certain conditions to the module category ${_{R}\mathsf {Mod}}$
over an associative ring $R$
, whose homotopy category is the $\mathcal {Q}$
-shaped derived category introduced by Holm and Jørgensen. Moreover, we prove that for an arbitrary associative ring $R$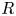
, an object in ${_{\mathcal {Q},\,R}\mathsf {Mod}}$
is Gorenstein projective (resp., Gorenstein injective, Gorenstein flat, projective coresolving Gorenstein flat) if and only if so is its value on each object of $\mathcal {Q}$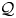
, and hence improve a result by Dell'Ambrogio, Stevenson and Šťovíček.
