This paper is concerned with a singular limit of the Kobayashi–Warren–Carter system, a phase field system modelling the evolutions of structures of grains. Under a suitable scaling, the limit system is formally derived when the interface thickness parameter tends to zero. Different from many other problems, it turns out that the limit system is a system involving fractional time derivatives, although the original system is a simple gradient flow. A rigorous derivation is given when the problem is reduced to a gradient flow of a single-well Modica–Mortola functional in a one-dimensional setting.

The connection between Residual Neural Networks (ResNets) and continuous-time control systems (known as NeurODEs) has led to a mathematical analysis of neural networks, which has provided interesting results of both theoretical and practical significance. However, by construction, NeurODEs have been limited to describing constant-width layers, making them unsuitable for modelling deep learning architectures with layers of variable width. In this paper, we propose a continuous-time Autoencoder, which we call AutoencODE, based on a modification of the controlled field that drives the dynamics. This adaptation enables the extension of the mean-field control framework originally devised for conventional NeurODEs. In this setting, we tackle the case of low Tikhonov regularisation, resulting in potentially non-convex cost landscapes. While the global results obtained for high Tikhonov regularisation may not hold globally, we show that many of them can be recovered in regions where the loss function is locally convex. Inspired by our theoretical findings, we develop a training method tailored to this specific type of Autoencoders with residual connections, and we validate our approach through numerical experiments conducted on various examples.

In the present paper we deal with a quasi-linear elliptic equation depending on a sublinear nonlinearity involving the gradient. We prove the existence of a nontrivial nodal solution employing the theory of invariant sets of descending flow together with sub-supersolution techniques, gradient regularity arguments, strong comparison principle for the $p$-Laplace operator. The same conclusion is obtained for an eigenvalue problem under a different set of assumptions.

Minimizing movements are investigated for an energy which is the superposition of a convex functional and fast small oscillations. Thus a minimizing movement scheme involves a temporal parameter τ and a spatial parameter ε, with τ describing the time step and the frequency of the oscillations being proportional to 1/ε. The extreme cases of fast time scales τ ≪ ε and slow time scales ε ≪ τ have been investigated in [4]. In this paper, the intermediate (critical) case of finite ratio ε/τ > 0 is studied. It is shown that a pinning threshold exists, with initial data below the threshold being a fixed point of the dynamics. A characterization of the pinning threshold is given. For initial data above the pinning threshold, the equation and velocity describing the homogenized motion are determined.

Let 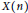$X\left( n \right)$, for 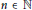$n\,\in \,\mathbb{N}$, be the set of all subsets of a metric space 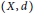$\left( x,\,d \right)$ of cardinality at most $n$. The set 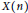$X\left( n \right)$ equipped with the Hausdorff metric is called a finite subset space. In this paper we are concerned with the existence of Lipschitz retractions 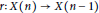$r:\,X\left( n \right)\,\to \,X\left( n\,-\,1 \right)$ for 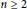$n\,\ge \,2$. It is known that such retractions do not exist if 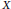$X$ is the one-dimensional sphere. On the other hand, Kovalev has recently established their existence if 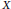$X$ is a Hilbert space, and he also posed a question as to whether or not such Lipschitz retractions exist when 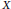$X$ is a Hadamard space. In this paper we answer the question in the positive.

We propose a positivity preserving entropy decreasing finite volume scheme for nonlinear nonlocal equations with a gradient flow structure. These properties allow for accurate computations of stationary states and long-time asymptotics demonstrated by suitably chosen test cases in which these features of the scheme are essential. The proposed scheme is able to cope with non-smooth stationary states, different time scales including metastability, as well as concentrations and self-similar behavior induced by singular nonlocal kernels. We use the scheme to explore properties of these equations beyond their present theoretical knowledge.

We study a Lagrangian numerical scheme for solution of a nonlinear drift diffusionequation on an interval. The discretization is based on the equation’s gradient flowstructure with respect to the Wasserstein distance. The scheme inherits various propertiesfrom the continuous flow, like entropy monotonicity, mass preservation, metric contractionand minimum/ maximum principles. As the main result, we give a proof of convergence in thelimit of vanishing mesh size under a CFL-type condition. We also present results fromnumerical experiments.

We extend results proved by the second author (Amer. J. Math., 2009) for nonnegatively curved Alexandrov spaces to general compact Alexandrov spaces $X$ with curvature bounded below. The gradient flow of a geodesically convex functional on the quadratic Wasserstein space $\left( \mathcal{P}\left( X \right),\,{{W}_{2}} \right)$ satisfies the evolution variational inequality. Moreover, the gradient flow enjoys uniqueness and contractivity. These results are obtained by proving a first variation formula for the Wasserstein distance.

We consider general surface energies, which areweighted integrals over a closed surface with a weight functiondepending on the position, the unit normal andthe mean curvature of the surface. Energiesof this form have applications in many areas, such as materials science,biology and image processing. Often one is interested in findinga surface that minimizes such an energy, which entails finding its firstvariation with respect to perturbations of the surface.We present a concise derivation of the first variation of thegeneral surface energy using tools from shape differential calculus.We first derive a scalar strong form and nexta vector weak form of the first variation. The latter reveals thevariational structure of the first variation, avoids dealingexplicitly with the tangential gradient of the unit normal,and thus can be easily discretized using parametric finite elements.Our results are valid for surfaces in any number of dimensionsand unify all previous results derived for specific examples ofsuch surface energies.

We investigate a global-in-time variational approach to abstract evolution by means of the weighted energy-dissipation functionals proposed by Mielke and Ortiz [ESAIM: COCV14 (2008) 494–516]. In particular, we focus on gradient flows in Hilbert spaces. The main result is the convergence of minimizers and approximate minimizers of these functionals to the unique solution of the gradient flow. Sharp convergence rates are provided and the convergence analysis is combined with time-discretization. Applications of the theory to various classes of parabolic PDE problems are presented. In particular, we focus on two examples of microstructure evolution from [S. Conti and M. Ortiz, J. Mech. Phys. Solids56 (2008) 1885–1904.].

This paper studies the gradient flow of a regularized Mumford-Shah functionalproposed by Ambrosio and Tortorelli (1990, 1992) for image segmentation, and adopted by Esedoglu and Shen (2002) for image inpainting. It is shown that the gradient flow with L2 x L∞ initial data possesses a global weak solution, and it has a unique global in timestrong solution, which has at most finite number of point singularities in the space-time, when the initial data are in H1 x H1 ∩ L∞ . A family of fully discrete approximation schemes using low order finite elements is proposed for the gradient flow. Convergence of a subsequence (resp. the whole sequence)of the numerical solutions to a weak solution (resp. the strong solution) of the gradient flow is established as the mesh sizes tend to zero, and optimal and suboptimal order error estimates, which depend on $\frac{1}{{\varepsilon}}$ and $\frac{1}{k_{\varepsilon}}$ only in low polynomial order, are derived for the proposed fully discrete schemes under the mesh relation $k=o(h^{\frac12})$ . Numerical experiments are also presented to show effectiveness of the proposed numerical methods and to validate the theoretical analysis.

We study the gradient flow for the total variation functional, which arises in image processing and geometric applications. We propose a variational inequality weak formulation for the gradient flow,and establish well-posedness of the problem by the energy method. The main idea of our approach is to exploit the relationship betweenthe regularized gradient flow (characterized by a small positive parameterε, see (1.7)) and the minimal surface flow [21]and the prescribed mean curvature flow [16].Since our approach is constructive and variational, finite element methods can be naturally applied to approximate weak solutions of the limiting gradient flow problem. We propose a fully discrete finite element method and establish convergence tothe regularized gradient flow problem as h,k → 0, and to the total variation gradient flow problem as h,k,ε → 0in general cases.Provided that the regularized gradient flow problem possessesstrong solutions, which is proved possible if the datum functionsare regular enough, we establish practical a priori error estimates for the fully discrete finite element solution, in particular, by focusing on the dependence of the error bounds on the regularization parameter ε. Optimal order error bounds are derived for the numerical solution under the meshrelation k = O(h2). In particular, it is shown thatall error bounds depend on $\frac{1}{\varepsilon}$ onlyin some lower polynomial order for small ε.