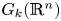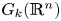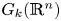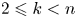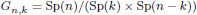6 results
Corrigendum to “Topological complexity of real Grassmannians”
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 19 April 2022, pp. 1071-1072
- Print publication:
- June 2023
-
- Article
-
- You have access
- HTML
- Export citation
On the topological complexity and zero-divisor cup-length of real Grassmannians
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 31 March 2022, pp. 702-717
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological complexity of real Grassmannians
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 12 January 2021, pp. 2013-2029
- Print publication:
- December 2021
-
- Article
- Export citation
Morse Theory and the Lusternik–Schnirelmann Category of Quaternionic Grassmannians
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 25 October 2016, pp. 441-449
-
- Article
- Export citation
Bayesian and geometric subspace tracking
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 43-56
- Print publication:
- March 2004
-
- Article
- Export citation
Darboux Transformations for the KP Hierarchy in the Segal-Wilson Setting
-
- Journal:
- Canadian Journal of Mathematics / Volume 53 / Issue 2 / 01 April 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 278-309
- Print publication:
- 01 April 2001
-
- Article
-
- You have access
- Export citation