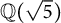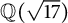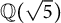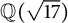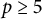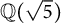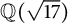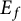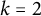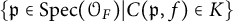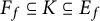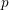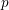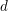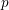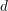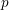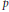14 results
Fermat’s Last Theorem over
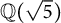 $\mathbb {Q}(\sqrt {\text{5}})$ and
$\mathbb {Q}(\sqrt {\text{5}})$ and 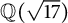 $\mathbb {Q}(\sqrt {\text{17}})$
$\mathbb {Q}(\sqrt {\text{17}})$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 21 November 2022, pp. 18-38
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
On generation of the coefficient field of a primitive Hilbert modular form by a single Fourier coefficient
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 08 September 2022, pp. 587-598
- Print publication:
- June 2023
-
- Article
- Export citation
GEOMETRIC WEIGHT-SHIFTING OPERATORS ON HILBERT MODULAR FORMS IN CHARACTERISTIC p
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 15 November 2021, pp. 1871-1930
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Explicit Serre weights for two-dimensional Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 1893-1907
- Print publication:
- September 2017
-
- Article
- Export citation
Minimal weights of Hilbert modular forms in characteristic
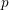 $p$
$p$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 13 June 2017, pp. 1769-1778
- Print publication:
- September 2017
-
- Article
- Export citation
Modularity of nearly ordinary 2-adic residually dihedral Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 8 / August 2014
- Published online by Cambridge University Press:
- 16 June 2014, pp. 1235-1346
- Print publication:
- August 2014
-
- Article
- Export citation
On the Kohnen plus space for Hilbert modular forms of half-integral weight I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 12 / December 2013
- Published online by Cambridge University Press:
- 06 September 2013, pp. 1963-2010
- Print publication:
- December 2013
-
- Article
- Export citation
On the Dihedral Main Conjectures of Iwasawa Theory for Hilbert Modular Eigenforms
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 2 / 01 April 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 403-466
- Print publication:
- 01 April 2013
-
- Article
-
- You have access
- Export citation
Level Raising and Anticyclotomic Selmer Groups for Hilbert Modular Forms of Weight Two
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 3 / 01 June 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 588-668
- Print publication:
- 01 June 2012
-
- Article
-
- You have access
- Export citation
Nonsolvable number fields ramified only at 3 and 5
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 15 February 2011, pp. 716-734
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
Hilbert modular forms and p-adic Hodge theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 21 September 2009, pp. 1081-1113
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
The exceptional zero conjecture for Hilbert modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 1-55
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
HILBERT MODULAR PSEUDODIFFERENTIAL OPERATORS OF MIXED WEIGHT
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 46 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 04 July 2003, pp. 269-277
-
- Article
-
- You have access
- Export citation
Adjoint L-Values and Primes of Congruence for Hilbert Modular Forms
-
- Journal:
- Compositio Mathematica / Volume 132 / Issue 3 / July 2002
- Published online by Cambridge University Press:
- 04 December 2007, pp. 243-281
- Print publication:
- July 2002
-
- Article
-
- You have access
- Export citation