Refine search
Actions for selected content:
86 results
Homogenization of vectorial free-discontinuity functionals with cohesive type surface terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-71
-
- Article
- Export citation
Homogenisation of Wasserstein gradient flows
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 29 July 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A dispersive effective equation for transverse propagation of planar shallow water waves over periodic bathymetry
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 15 May 2025, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
12 - Multi-Scale Modeling of Composite Structures Using Computational Grains
-
- Book:
- Computational Grains
- Published online:
- 05 October 2023
- Print publication:
- 19 October 2023, pp 237-273
-
- Chapter
- Export citation
The effect of high-temperature heat treatment and homogenization on the microstructure of set yogurt curd networks
-
- Journal:
- Journal of Dairy Research / Volume 90 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 31 August 2023, pp. 306-311
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wasserstein convergence rates in the invariance principle for deterministic dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 June 2023, pp. 1172-1191
- Print publication:
- April 2024
-
- Article
- Export citation
1 - Multilingualism
-
- Book:
- Multilingual Development
- Published online:
- 17 January 2023
- Print publication:
- 05 January 2023, pp 1-43
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Industrialization and Assimilation
- Published online:
- 18 November 2022
- Print publication:
- 22 December 2022, pp 1-21
-
- Chapter
- Export citation
Dirichlet vs Neumann
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 22 November 2022, pp. 1063-1074
-
- Article
- Export citation

Industrialization and Assimilation
- Understanding Ethnic Change in the Modern World
-
- Published online:
- 18 November 2022
- Print publication:
- 22 December 2022
11 - Composite Networks
-
- Book:
- Network Materials
- Published online:
- 15 September 2022
- Print publication:
- 22 September 2022, pp 393-427
-
- Chapter
- Export citation
23 - Nationalist Ethos, Collective Reformation, and Citizenry Power
- from Part V - Reforms and Revolutions
-
- Book:
- Understanding Modern Nigeria
- Published online:
- 09 June 2021
- Print publication:
- 24 June 2021, pp 561-577
-
- Chapter
- Export citation
5 - Cultural Diversity and Coercive Cultural Homogenization in Chinese History
- from Part II - Historical Orders
-
-
- Book:
- Culture and Order in World Politics
- Published online:
- 25 December 2019
- Print publication:
- 09 January 2020, pp 93-112
-
- Chapter
- Export citation
4 - Numerical Homogenization
- from Part I - The Sobolev Space Setting
-
- Book:
- Operator-Adapted Wavelets, Fast Solvers, and Numerical Homogenization
- Published online:
- 10 October 2019
- Print publication:
- 24 October 2019, pp 38-62
-
- Chapter
- Export citation
Cauchy problem and periodic homogenization for nonlocal Hamilton–Jacobi equations with coercive gradient terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 17 September 2019, pp. 3028-3059
- Print publication:
- December 2020
-
- Article
- Export citation
Asymptotic Behaviour of the Energy Integral of a Two-Parameter Homogenization Problem with Nonlinear Periodic Robin Boundary Conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 22 March 2019, pp. 985-1016
-
- Article
- Export citation
First-order expansions for eigenvalues and eigenfunctions in periodic homogenization
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 20 March 2019, pp. 2189-2215
- Print publication:
- October 2020
-
- Article
- Export citation
Convergence of equilibria for bending-torsion models of rods with inhomogeneities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 January 2019, pp. 233-260
- Print publication:
- February 2020
-
- Article
- Export citation
Deformation-controlled cation diffusion in compositionally zoned tourmaline
-
- Journal:
- Mineralogical Magazine / Volume 69 / Issue 4 / August 2005
- Published online by Cambridge University Press:
- 05 July 2018, pp. 471-489
-
- Article
- Export citation
Heterogeneity and strong competition in ecology
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 25 June 2018, pp. 682-706
-
- Article
- Export citation
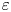
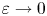
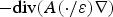
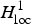
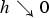
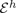 , for a rod
, for a rod 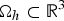
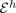 , provided that the bending energy of the sequence scales appropriately. This generalizes earlier results for homogeneous materials to the case of materials with (not necessarily periodic) inhomogeneities.
, provided that the bending energy of the sequence scales appropriately. This generalizes earlier results for homogeneous materials to the case of materials with (not necessarily periodic) inhomogeneities.