15 results
Stability properties of multidimensional symmetric hyperbolic systems with damping, differential constraints and delay
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 September 2023, pp. 1-43
-
- Article
- Export citation
DRAPING WOVEN SHEETS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 07 January 2021, pp. 355-385
-
- Article
- Export citation
Cohomology of fiber-bunched twisted cocycles over hyperbolic systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 21 July 2020, pp. 844-860
-
- Article
- Export citation
Existence and linearized stability of solitary waves for a quasilinear Benney system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 21 March 2016, pp. 547-564
- Print publication:
- June 2016
-
- Article
- Export citation
The Space-Time CE/SE Method for Solving Reduced Two-Fluid Flow Model
-
- Journal:
- Communications in Computational Physics / Volume 12 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 1070-1095
- Print publication:
- October 2012
-
- Article
- Export citation
Modelling and simulation of liquid-vapor phase transition incompressible flows based on thermodynamical equilibrium∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 46 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 13 February 2012, pp. 1029-1054
- Print publication:
- September 2012
-
- Article
- Export citation
Numerical Entropy and Adaptivity for Finite Volume Schemes
-
- Journal:
- Communications in Computational Physics / Volume 10 / Issue 5 / November 2011
- Published online by Cambridge University Press:
- 20 August 2015, pp. 1132-1160
- Print publication:
- November 2011
-
- Article
- Export citation
Indirect stabilization of locally coupled wave-type systems
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 14 September 2011, pp. 548-582
- Print publication:
- April 2012
-
- Article
- Export citation
Relaxation and numerical approximation of a two-fluid two-pressure diphasic model
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 43 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 09 October 2009, pp. 1063-1097
- Print publication:
- November 2009
-
- Article
- Export citation
Analysis of lumped parameter models for blood flow simulations and their relation with 1D models
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 4 / July 2004
- Published online by Cambridge University Press:
- 15 August 2004, pp. 613-632
- Print publication:
- July 2004
-
- Article
- Export citation
On the analysis of Bérenger's Perfectly Matched Layers for Maxwell's equations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 1 / January 2002
- Published online by Cambridge University Press:
- 15 April 2002, pp. 87-119
- Print publication:
- January 2002
-
- Article
- Export citation
Local controllability of a 1-D tank containing a fluid modeled by the shallow water equations
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 8 / 2002
- Published online by Cambridge University Press:
- 15 August 2002, pp. 513-554
- Print publication:
- 2002
-
- Article
- Export citation
A steady-state capturing method for hyperbolic systems with geometrical source terms
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 35 / Issue 4 / July 2001
- Published online by Cambridge University Press:
- 15 April 2002, pp. 631-645
- Print publication:
- July 2001
-
- Article
- Export citation
Rigorous derivation of Korteweg-de Vries-type systems from a general class of nonlinear hyperbolic systems
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 34 / Issue 4 / July 2000
- Published online by Cambridge University Press:
- 15 April 2002, pp. 873-911
- Print publication:
- July 2000
-
- Article
- Export citation
The Accuracy and Coverage of Loran-C and of the Decca Navigator System — and the Fallacy of Fixed Errors
-
- Journal:
- The Journal of Navigation / Volume 45 / Issue 1 / January 1992
- Published online by Cambridge University Press:
- 21 October 2009, pp. 36-51
- Print publication:
- January 1992
-
- Article
- Export citation

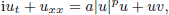
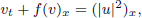
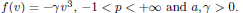 , –1 <
, –1 < 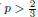 . We also show the existence of standing waves in the case
. We also show the existence of standing waves in the case 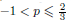 , with compact support if – 1 <
, with compact support if – 1 < 