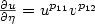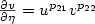Research Article
Isoparametric mixed finite element approximation of eigenvalues and eigenvectors of 4th order eigenvalue problems with variable coefficients
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 1-32
-
- Article
- Export citation
On the convergence rate of approximation schemes forHamilton-Jacobi-Bellman Equations
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 33-54
-
- Article
- Export citation
Simultaneous vs. non-simultaneous blow-up in numerical approximations of aparabolic system with non-linear boundary conditions
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 55-68
-
- Article
- Export citation
Coupling of transport and diffusion models in linear transport theory
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 69-86
-
- Article
- Export citation
On the analysis of Bérenger's Perfectly Matched Layers for Maxwell's equations
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 87-119
-
- Article
- Export citation
A modal synthesis method for the elastoacoustic vibrationproblem
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 121-142
-
- Article
- Export citation
Numerical analysis of nonlinear elliptic-parabolic equations
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 143-153
-
- Article
- Export citation