We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In [5], a particular family of real hyperplane arrangements stemming from hyperpolygonal spaces associated with certain quiver varieties was introduced which we thus call hyperpolygonal arrangements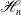 
${\mathscr H}_n$. In this note, we study these arrangements and investigate their properties systematically. Remarkably, the arrangements 
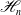${\mathscr H}_n$ discriminate between essentially all local properties of arrangements. In addition, we show that hyperpolygonal arrangements are projectively unique and combinatorially formal.
We note that the arrangement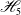 
${\mathscr H}_5$ is the famous counterexample of Edelman and Reiner [17] of Orlik’s conjecture that the restriction of a free arrangement is again free.
