Refine search
Actions for selected content:
2 results
Note on generalizations of Mecke's formula and extensions of H = λG
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 105-122
- Print publication:
- March 1995
-
- Article
- Export citation
Generalised birth and death queueing processes: recent results
-
- Journal:
- Advances in Applied Probability / Volume 9 / Issue 1 / March 1977
- Published online by Cambridge University Press:
- 01 July 2016, pp. 125-140
- Print publication:
- March 1977
-
- Article
- Export citation
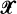 , and relates integrations concerning them to each other. For
, and relates integrations concerning them to each other. For 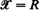 , we generalize this to a pair of random measures which are jointly stationary. The resulting formula extends the so-called Swiss Army formula, which was recently obtained as a generalization for Little's formula. The generalized Mecke formula, which is called GMF, can be also viewed as a generalization of the stationary version of
, we generalize this to a pair of random measures which are jointly stationary. The resulting formula extends the so-called Swiss Army formula, which was recently obtained as a generalization for Little's formula. The generalized Mecke formula, which is called GMF, can be also viewed as a generalization of the stationary version of 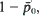 where
where 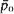 is the stable probability of an empty system, consistent with other systems. It is also shown that for first come, first served discipline the equivalent
is the stable probability of an empty system, consistent with other systems. It is also shown that for first come, first served discipline the equivalent 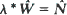 of Little's formula holds, where
of Little's formula holds, where 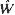 and
and 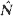 are the mean waiting time of an arrival and mean system size at an arbitrary epoch. In addition it appears that stable regime output intervals are statistically identical with effective inter-arrival intervals. Symmetrical moment formulae of arbitrary order are derived algebraically for effective inter-arrival and service intervals, for waiting time, for busy period and for output.
are the mean waiting time of an arrival and mean system size at an arbitrary epoch. In addition it appears that stable regime output intervals are statistically identical with effective inter-arrival intervals. Symmetrical moment formulae of arbitrary order are derived algebraically for effective inter-arrival and service intervals, for waiting time, for busy period and for output.