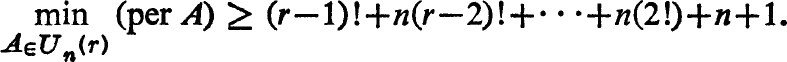14 results
Quantile Lower Bounds to Reliability Based on Locally Optimal Splits
-
- Journal:
- Psychometrika / Volume 80 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 01 January 2025, pp. 182-195
-
- Article
- Export citation
The lower bounds of non-real eigenvalues for singular indefinite Sturm–Liouville problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 December 2023, pp. 1-10
-
- Article
- Export citation
2 - Lower Bounds and a Property of Λ
-
- Book:
- Large Deviations for Markov Chains
- Published online:
- 03 August 2022
- Print publication:
- 27 October 2022, pp 14-35
-
- Chapter
- Export citation
4 - Gradient Methods Using Momentum
-
- Book:
- Optimization for Data Analysis
- Published online:
- 31 March 2022
- Print publication:
- 21 April 2022, pp 55-74
-
- Chapter
- Export citation
13 - Distributed Computing
- from Part II - Applications
-
- Book:
- Communication Complexity
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp 239-243
-
- Chapter
- Export citation
12 - Extension Complexity of Polytopes
- from Part II - Applications
-
- Book:
- Communication Complexity
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp 210-238
-
- Chapter
- Export citation
6 - Leray’s fundamental work on the Navier–Stokes equations: a modern review of “Sur le mouvement d’un liquide visqueux emplissant l’espace”
-
- Book:
- Partial Differential Equations in Fluid Mechanics
- Published online:
- 15 August 2019
- Print publication:
- 27 September 2018, pp 113-203
-
- Chapter
- Export citation
Méthode heuristique pour le problème de flow shop hybride avec machines dédiées
-
- Journal:
- RAIRO - Operations Research / Volume 43 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 08 October 2009, pp. 421-436
- Print publication:
- October 2009
-
- Article
- Export citation
Incorporating the strength of MIP modeling in schedule construction
-
- Journal:
- RAIRO - Operations Research / Volume 43 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 08 October 2009, pp. 409-420
- Print publication:
- October 2009
-
- Article
- Export citation
Characterizing the Complexity of Boolean Functions represented by Well-Structured Graph-Driven Parity-FBDDs
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 36 / Issue 3 / July 2002
- Published online by Cambridge University Press:
- 15 December 2002, pp. 229-247
- Print publication:
- July 2002
-
- Article
- Export citation
A Space Lower Bound for Acceptance by One-Way Π2-Alternating Machines
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 34 / Issue 5 / September 2000
- Published online by Cambridge University Press:
- 15 April 2002, pp. 357-372
- Print publication:
- September 2000
-
- Article
- Export citation
Bonferroni bounds revisited
-
- Journal:
- Journal of Applied Probability / Volume 26 / Issue 2 / June 1989
- Published online by Cambridge University Press:
- 14 July 2016, pp. 233-241
- Print publication:
- June 1989
-
- Article
- Export citation
A Canonical Form For Fully Indecomposable (0,1)-Matrices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 18 / Issue 2 / June 1975
- Published online by Cambridge University Press:
- 20 November 2018, pp. 223-227
- Print publication:
- June 1975
-
- Article
-
- You have access
- Export citation
A Lower Bound for the Permanent on a Special Class of Matrices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 17 / Issue 4 / 01 December 1974
- Published online by Cambridge University Press:
- 20 November 2018, pp. 529-530
- Print publication:
- 01 December 1974
-
- Article
-
- You have access
- Export citation