A language L ⊆A* is literally idempotent in case that ua2v ∈ L if and only if uav ∈ L, for each u,v ∈ A*, a ∈ A. Varieties of literally idempotent languages result naturally by taking all literally idempotent languages in a classical (positive) variety or by considering a certain closure operator on classes of languages. We initiate the systematic study of such varieties. Various classes of literally idempotent languages can be characterized using syntactic methods. A starting example is the class of all finite unions of $B^*_1 B^*_2\dots B^*_k$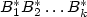 where B1,...,Bk are subsets of a given alphabet A.