This article is devoted to the study of some high-order difference schemes for the distributed-order time-fractional equations in both one and two space dimensions. Based on the composite Simpson formula and Lubich second-order operator, a difference scheme is constructed with 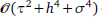 convergence in the L1(L∞)-norm for the one-dimensional case, where τ,h and σ are the respective step sizes in time, space and distributed-order. Unconditional stability and convergence are proven. An ADI difference scheme is also derived for the two-dimensional case, and proven to be unconditionally stable and
convergence in the L1(L∞)-norm for the one-dimensional case, where τ,h and σ are the respective step sizes in time, space and distributed-order. Unconditional stability and convergence are proven. An ADI difference scheme is also derived for the two-dimensional case, and proven to be unconditionally stable and 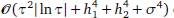 convergent in the L1(L∞)-norm, where h1 and h2 are the spatial step sizes. Some numerical examples are also given to demonstrate our theoretical results.
convergent in the L1(L∞)-norm, where h1 and h2 are the spatial step sizes. Some numerical examples are also given to demonstrate our theoretical results.

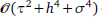 convergence in the L
convergence in the L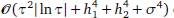 convergent in the L
convergent in the L