6 results
Differentiability of the operator norm on \ell _p spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 December 2024, pp. 1-20
-
- Article
-
- You have access
- HTML
- Export citation
Ideals with approximate unit in semicrossed products
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 12 September 2023, pp. 257-264
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIRKHOFF ORTHOGONALITY IN CLASSICAL M-IDEALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 08 November 2016, pp. 279-288
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Ideals of compact operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 91-110
- Print publication:
- August 2004
-
- Article
-
- You have access
- Export citation
A Note on M-Ideals of Compact operators
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 4 / 01 December 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 434-440
- Print publication:
- 01 December 1989
-
- Article
-
- You have access
- Export citation
A Note on M-Summands in Dual Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 30 / Issue 4 / 01 December 1987
- Published online by Cambridge University Press:
- 20 November 2018, pp. 393-398
- Print publication:
- 01 December 1987
-
- Article
-
- You have access
- Export citation

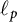
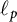
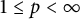
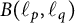
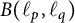
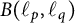
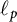
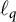
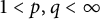
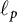
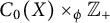
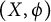
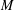
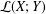
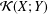
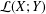
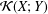
 (
(
