 $\mathbb {Z}$-COVERS OF A FINITE GRAPH AND MAHLER MEASURES
$\mathbb {Z}$-COVERS OF A FINITE GRAPH AND MAHLER MEASURES
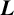 $\boldsymbol {L}$
-VALUES
$\boldsymbol {L}$
-VALUES
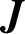 $\boldsymbol {J}$
-BESSEL FUNCTIONS AND ITS APPLICATION TO MAHLER MEASURE
$\boldsymbol {J}$
-BESSEL FUNCTIONS AND ITS APPLICATION TO MAHLER MEASURE