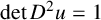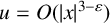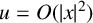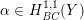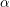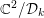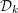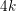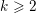4 results
THE GROWTH OF SOLUTIONS OF MONGE–AMPÈRE EQUATIONS IN HALF SPACES AND ITS APPLICATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 31 March 2023, pp. 125-137
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
Geometry and topology of the space of Kähler metrics on singular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 8 / August 2018
- Published online by Cambridge University Press:
- 19 July 2018, pp. 1593-1632
- Print publication:
- August 2018
-
- Article
- Export citation
From ALE to ALF gravitational instantons
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 1159-1221
- Print publication:
- June 2018
-
- Article
- Export citation
REGULARITY OF MONGE–AMPÈRE EQUATIONS IN OPTIMAL TRANSPORTATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 27 January 2011, pp. 173-176
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation