We state and prove a Korn-like inequality for a vector field in abounded open set of $\mathbb{R}^N$ 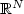 , satisfying a tangency boundary condition.This inequality, which is crucial in our study of the trend towardsequilibrium for dilute gases, holds true if and only if the domain is notaxisymmetric. We give quantitative, explicit estimates on how thedeparture from axisymmetry affects the constants; a Monge–Kantorovichminimization problem naturally arises in this process. Variants in the axisymmetric case are briefly discussed.
, satisfying a tangency boundary condition.This inequality, which is crucial in our study of the trend towardsequilibrium for dilute gases, holds true if and only if the domain is notaxisymmetric. We give quantitative, explicit estimates on how thedeparture from axisymmetry affects the constants; a Monge–Kantorovichminimization problem naturally arises in this process. Variants in the axisymmetric case are briefly discussed.