Refine search
Actions for selected content:
17 results
6 - The Power Spectrum
-
- Book:
- Statistical Methods for Climate Scientists
- Published online:
- 03 February 2022
- Print publication:
- 24 February 2022, pp 126-155
-
- Chapter
- Export citation
9 - Periodograms and Significance
-
- Book:
- A Primer on Fourier Analysis for the Geosciences
- Published online:
- 01 February 2019
- Print publication:
- 14 February 2019, pp 137-158
-
- Chapter
- Export citation

A Primer on Fourier Analysis for the Geosciences
-
- Published online:
- 01 February 2019
- Print publication:
- 14 February 2019
Goodness-of-fit tests in long-range dependent processes under fixed alternatives
-
- Journal:
- ESAIM: Probability and Statistics / Volume 17 / 2013
- Published online by Cambridge University Press:
- 21 May 2013, pp. 432-443
- Print publication:
- 2013
-
- Article
- Export citation
Goodness-of-fit test for long range dependent processes
-
- Journal:
- ESAIM: Probability and Statistics / Volume 6 / 2002
- Published online by Cambridge University Press:
- 15 November 2002, pp. 239-258
- Print publication:
- 2002
-
- Article
- Export citation
Efficient estimation of functionals of the spectraldensity of stationary Gaussian fields
-
- Journal:
- ESAIM: Probability and Statistics / Volume 3 / 1999
- Published online by Cambridge University Press:
- 15 August 2002, pp. 23-47
- Print publication:
- 1999
-
- Article
- Export citation
Discrimination between monotonic trends and long-range dependence
-
- Journal:
- Journal of Applied Probability / Volume 23 / Issue 4 / December 1986
- Published online by Cambridge University Press:
- 24 August 2016, pp. 1025-1030
- Print publication:
- December 1986
-
- Article
- Export citation
Regression for randomly sampled spatial series: the trigonometric case
-
- Journal:
- Journal of Applied Probability / Volume 23 / Issue A / 1986
- Published online by Cambridge University Press:
- 14 July 2016, pp. 275-289
- Print publication:
- 1986
-
- Article
- Export citation
On the asymptotic distributions of maxima of trigonometric polynomials with random coefficients
-
- Journal:
- Advances in Applied Probability / Volume 16 / Issue 4 / December 1984
- Published online by Cambridge University Press:
- 01 July 2016, pp. 819-842
- Print publication:
- December 1984
-
- Article
- Export citation
On the estimation of frequency in point-process data
-
- Journal:
- Journal of Applied Probability / Volume 19 / Issue A / 1982
- Published online by Cambridge University Press:
- 14 July 2016, pp. 383-394
- Print publication:
- 1982
-
- Article
- Export citation
On the spectral decomposition of stationary time series using walsh functions. I
-
- Journal:
- Advances in Applied Probability / Volume 12 / Issue 1 / March 1980
- Published online by Cambridge University Press:
- 01 July 2016, pp. 183-199
- Print publication:
- March 1980
-
- Article
- Export citation
On estimation of the integrals of certain functions of spectral density
-
- Journal:
- Journal of Applied Probability / Volume 17 / Issue 1 / March 1980
- Published online by Cambridge University Press:
- 14 July 2016, pp. 73-83
- Print publication:
- March 1980
-
- Article
- Export citation
On estimation of parameters of Gaussian stationary processes
-
- Journal:
- Journal of Applied Probability / Volume 16 / Issue 3 / September 1979
- Published online by Cambridge University Press:
- 14 July 2016, pp. 575-591
- Print publication:
- September 1979
-
- Article
- Export citation
Testing the hypothesis that a point is Poisson
-
- Journal:
- Advances in Applied Probability / Volume 9 / Issue 4 / December 1977
- Published online by Cambridge University Press:
- 01 July 2016, pp. 724-746
- Print publication:
- December 1977
-
- Article
- Export citation
Gordin's theorem and the periodogram
-
- Journal:
- Journal of Applied Probability / Volume 13 / Issue 2 / June 1976
- Published online by Cambridge University Press:
- 14 July 2016, pp. 365-370
- Print publication:
- June 1976
-
- Article
- Export citation
Asymptotic properties of certain functionals of the periodogram
-
- Journal:
- Journal of Applied Probability / Volume 11 / Issue 3 / September 1974
- Published online by Cambridge University Press:
- 14 July 2016, pp. 578-581
- Print publication:
- September 1974
-
- Article
- Export citation
Asymptotic inference in stationary Gaussian time-series
-
- Journal:
- Advances in Applied Probability / Volume 5 / Issue 3 / December 1973
- Published online by Cambridge University Press:
- 01 July 2016, pp. 469-497
- Print publication:
- December 1973
-
- Article
- Export citation
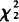 -distribution with noncentrality parameter tending to 0 uniformly outside intervals
-distribution with noncentrality parameter tending to 0 uniformly outside intervals 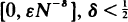 . In the latter case it has λ
. In the latter case it has λ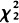 -distribution, 0 <
-distribution, 0 < 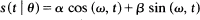
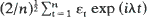 exp
exp 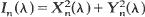 . It is shown that as
. It is shown that as 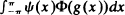 whose asymptotic variance is
whose asymptotic variance is 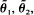 by minimizing two criteria
by minimizing two criteria 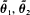 with respect to efficiency and robustness.
with respect to efficiency and robustness.