Pareto distribution is an important distribution in extreme value theory. In this paper, we consider parallel systems with Pareto components and study the effect of heterogeneity on skewness of such systems. It is shown that, when the lifetimes of components have different shape parameters, the parallel system with heterogeneous Pareto component lifetimes is more skewed than the system with independent and identically distributed Pareto components. However, for the case when the lifetimes of components have different scale parameters, the result gets reversed in the sense of star ordering. We also establish the relation between star ordering and dispersive ordering by extending the result of Deshpande and Kochar [(1983). Dispersive ordering is the same as tail ordering. Advances in Applied Probability 15(3): 686–687] from support $(0, \infty )$ to general supports $(a, \infty )$, $a > 0$. As a consequence, we obtain some new results on dispersion of order statistics from heterogeneous Pareto samples with respect to dispersive ordering.

In this paper, we discuss stochastic orderings of lifetimes of two heterogeneous parallel and series systems with heterogeneous dependent components having generalized Birnbaum–Saunders distributions. The comparisons presented here are based on the vector majorization of parameters. The ordering results are established in some special cases for the generalized Birnbaum–Saunders distribution based on the multivariate elliptical, normal, t, logistic, and skew-normal kernels. Further, we use these results by considering Archimedean copulas to model the dependence structure among systems with generalized Birnbaum–Saunders components. These results have been used to derive some upper and lower bounds for survival functions of lifetimes of parallel and series systems.

This paper studies the variability of both series and parallel systems comprised of heterogeneous (and dependent) components. Sufficient conditions are established for the star and dispersive orderings between the lifetimes of parallel [series] systems consisting of dependent components having multiple-outlier proportional hazard rates and Archimedean [Archimedean survival] copulas. We also prove that, without any restriction on the scale parameters, the lifetime of a parallel or series system with independent heterogeneous scaled components is larger than that with independent homogeneous scaled components in the sense of the convex transform order. These results generalize some corresponding ones in the literature to the case of dependent scenarios or general settings of components lifetime distributions.

Mao and Hu (2010) left an open problem about the hazard rate order between the largest order statistics from two samples of n geometric random variables. Du et al. (2012) solved this open problem when n = 2, and Wang (2015) solved for 2 ≤ n ≤ 9. In this paper we completely solve this problem for any value of n.

In this paper we provide a sufficient condition for mean residual life ordering of parallel systems with n ≥ 3 heterogeneous exponential components.

This paper considers stochastic comparison of parallel systems in terms of likelihood ratio order under scale models. We introduce a new order, the so-called q-larger order, and show that under certain conditions, the q-larger order between the scale vectors can imply the likelihood ratio order of parallel systems. Applications are given to the generalized gamma scale family.

We consider the problem of reducing the response time of fork-join systems by maintaining the workload balanced among the processing stations. The general problem of modeling and finding an optimal policy that reduces imbalance is quite difficult. In order to circumvent this difficulty, the heavy traffic approach is taken, and the system dynamics are approximated by a reflected diffusion process. This way, the problem of finding an optimal balancing policy that reduces workload imbalance is set as a stochastic optimal control problem, for which numerical methods are available. Some numerical experiments are presented, where the control problem is solved numerically and applied to a simulation. The results indicate that the response time of the controlled system is reduced significantly using the devised control.

The signature is an important structural characteristic of a coherent system. Its computation, however, is often rather involved and complex. We analyze several cases where this complexity can be considerably reduced. These are the cases when a ‘large’ coherent system is obtained as a series, parallel, or recurrent structure built from ‘small’ modules with known signature. Corresponding formulae can be obtained in terms of cumulative notions of signatures. An algebraic closure property of families of homogeneous polynomials plays a substantial role in our derivations.

In this paper, we investigate k-out-of-n systems with independent and identically distributed components. Some characterizations of the IFR(2), DMRL, NBU(2) and NBUC classes of life distributions are obtained in terms of the monotonicity of the residual life given that the (n-k)th failure has occurred at time t ≥ 0. These results complement those reported by Belzunce, Franco and Ruiz (1999). Similar conclusions based on the residual life of a parallel system conditioned by the (n-k)th failure time are presented as well.

We study a reliability system subject to shocks generated by a renewal point process. When a shock occurs, components fail independently of each other with equal probabilities that are random numbers drawn from a distribution that may differ from shock to shock. We first consider the case of a parallel system and derive closed expressions for the Laplace-Stieltjes transform and the expectation of the time to system failure and for its density in the case that the distribution function of the renewal process possesses a density. We then treat a more general system structure, which has some very important special cases, such as k-out-of-n:F systems, and derive analogous formulae.

In this paper we study the problem of computing the downtime distribution of a parallel system comprising stochastically identical components. It is assumed that the components are independent, with an exponential life-time distribution and an arbitrary repair time distribution. An exact formula is established for the distribution of the system downtime given a specific type of system failure scenario. It is shown by performing a Monte Carlo simulation that the portion of the system failures that occur as described by this scenario is close to one when we consider a system with quite available components, the most common situation in practice. Thus we can use the established formula as an approximation of the downtime distribution given system failure. The formula is compared with standard Markov expressions. Some possible extensions of the formula are presented.

The concept of max-infinite divisibility is viewed as a positive dependence concept. It is shown that every max-infinitely divisible distribution function is a multivariate totally positive function of order 2 (MTP2). Inequalities are derived, with emphasis on exchangeable distributions. Applications and examples are given throughout the paper.

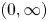
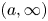
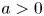
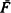Two arbitrary life distributions F and G can be ordered with respect to their Laplace transforms. We say is Laplace-smaller than 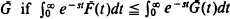for all s > 0. Interpretations of this ordering concept in reliability, operations research, and economics are described. General preservation properties are presented. Using these preservation results we derive useful inequalities and discuss their applications to M/G/1 queues, time series, coherent systems, shock models and cumulative damage models.

This paper considers a problem of determining the optimal number of units for a parallel redundant system. The optimal number N∗ to minimize the expected cost is given by a unique solution of equations. When the system is replaced before failure at time T, the optimal N∗ and T∗ are discussed, and a computing procedure for obtaining these values is specified.

We have recently discussed the replacement problem of a parallel system in a random environment. This paper extends the same replacement problem for the following two cases which are more plausible: (i) The probability that an operating component fails by the j th shock depends on the number j. (ii) The replacement cost is a linear function of failed components. The expected cost of the above model is obtained. A numerical example is finally presented when the probability of failure time of a component is a negative binomial distribution.

Råde considered a parallel system with n components in a random environment. The shocks cause the components to fail with certain probabilities. This paper considers the replacement policy for the above system in which it is exchanged before failure if the total number of failed components is more than k, and it is replaced if all of n components have failed. An optimum number of k which will minimize the expected cost is obtained. A numerical example is finally presented.

A parallel reliability system is subject to shocks which are generated by a renewal point process. The shocks cause the components to fail with certain probabilities. First we study the case when the components fail independently of each other with the same probability. For this case simple closed expressions for the Laplace-Stieltjes transform and expectation of time to system failure are derived. Then a case of dependent components is studied: the probability of failure of a component depends on the number of functioning components. Some extensions are mentioned.