12 results
STABLE ORDERED UNION ULTRAFILTERS AND cov
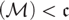 $\left( \mathcal{M} \right) < \mathfrak{c}$
$\left( \mathcal{M} \right) < \mathfrak{c}$
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 April 2019, pp. 1176-1193
- Print publication:
- September 2019
-
- Article
- Export citation
WOODIN FOR STRONG COMPACTNESS CARDINALS
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 14 March 2019, pp. 301-319
- Print publication:
- March 2019
-
- Article
- Export citation
THE HARRINGTON–SHELAH MODEL WITH LARGE CONTINUUM
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 22 February 2019, pp. 684-703
- Print publication:
- June 2019
-
- Article
- Export citation
NORMAL MEASURES ON A TALL CARDINAL
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 178-204
- Print publication:
- March 2019
-
- Article
- Export citation
SOME APPLICATIONS OF SUPERCOMPACT EXTENDER BASED FORCINGS TO HOD
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 461-476
- Print publication:
- June 2018
-
- Article
- Export citation
THE EIGHTFOLD WAY
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 01 May 2018, pp. 349-371
- Print publication:
- March 2018
-
- Article
- Export citation
SQUARES AND NARROW SYSTEMS
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 834-859
- Print publication:
- September 2017
-
- Article
- Export citation
PRODUCTS OF HUREWICZ SPACES IN THE LAVER MODEL
-
- Journal:
- Bulletin of Symbolic Logic / Volume 23 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 04 December 2017, pp. 324-333
- Print publication:
- September 2017
-
- Article
- Export citation
DENSE IDEALS AND CARDINAL ARITHMETIC
-
- Journal:
- The Journal of Symbolic Logic / Volume 81 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 14 September 2016, pp. 789-813
- Print publication:
- September 2016
-
- Article
- Export citation
Filter games and pathological subgroups of a countable product of lines
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 3 / December 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 321-350
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Possible behaviours of the reflection ordering of stationary sets
-
- Journal:
- The Journal of Symbolic Logic / Volume 60 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 12 March 2014, pp. 534-547
- Print publication:
- June 1995
-
- Article
- Export citation
Full reflection at a measurable cardinal
-
- Journal:
- The Journal of Symbolic Logic / Volume 59 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 12 March 2014, pp. 615-630
- Print publication:
- June 1994
-
- Article
- Export citation

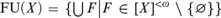
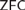
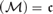
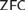
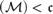
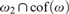
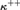
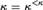
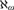
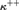
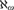
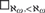
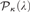
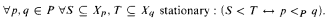
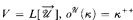 , and
, and 