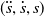26 results
Projecting robot dynamics onto trajectories
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
4 - Basic Real Algebraic Geometry in Rd
-
- Book:
- Polynomial Methods and Incidence Theory
- Published online:
- 17 March 2022
- Print publication:
- 24 March 2022, pp 51-65
-
- Chapter
- Export citation
3 - Assessing Climate-Change Impacts at the Regional Scale
-
- Book:
- Downscaling Techniques for High-Resolution Climate Projections
- Published online:
- 05 February 2021
- Print publication:
- 11 February 2021, pp 40-63
-
- Chapter
- Export citation
10 - Geometric Constructions
- from Part Two - Examples
-
- Book:
- Assouad Dimension and Fractal Geometry
- Published online:
- 13 October 2020
- Print publication:
- 29 October 2020, pp 160-180
-
- Chapter
- Export citation
Number of dementia sufferers in Europe between the years 2000 and 2050
-
- Journal:
- European Psychiatry / Volume 18 / Issue 6 / October 2003
- Published online by Cambridge University Press:
- 16 April 2020, pp. 306-313
-
- Article
- Export citation
The implications of demographic and economic projections on public pension spending in the European Union
-
- Journal:
- Journal of International and Comparative Social Policy / Volume 34 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 09 March 2020, pp. 19-39
-
- Article
- Export citation
Appendix - Miscellaneous background
-
- Book:
- Tensor Products of <I>C</I>*-Algebras and Operator Spaces
- Published online:
- 10 February 2020
- Print publication:
- 27 February 2020, pp 438-469
-
- Chapter
- Export citation
14 - Gosset–Elte Polytopes
- from IV - Miscellaneous Polytopes
-
- Book:
- Geometric Regular Polytopes
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp 477-505
-
- Chapter
- Export citation
6 - Applications
-
- Book:
- Wigner-Type Theorems for Hilbert Grassmannians
- Published online:
- 06 January 2020
- Print publication:
- 16 January 2020, pp 125-140
-
- Chapter
- Export citation
On a Linear Refinement of the Prékopa-Leindler Inequality
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 4 / 01 August 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 762-783
- Print publication:
- 01 August 2016
-
- Article
-
- You have access
- Export citation
Optimizing phylogenetic supertrees using answer set programming
-
- Journal:
- Theory and Practice of Logic Programming / Volume 15 / Issue 4-5 / July 2015
- Published online by Cambridge University Press:
- 03 September 2015, pp. 604-619
-
- Article
- Export citation
NONLINEAR ANALYSIS IN GEODESIC METRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 05 August 2015, pp. 514-515
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Impacts of Incorporating Land Exchanges Between Forestry and Agriculture in Sector Models
-
- Journal:
- Journal of Agricultural and Applied Economics / Volume 30 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 28 April 2015, pp. 389-401
-
- Article
- Export citation
ON SMALL SUBSPACE LATTICES IN HILBERT SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 15 October 2013, pp. 44-60
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
A growing care gap? The supply of unpaid care for older people by their adult children in England to 2032
-
- Journal:
- Ageing & Society / Volume 35 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 22 August 2013, pp. 96-123
- Print publication:
- January 2015
-
- Article
-
- You have access
- HTML
- Export citation
Stability and Separation in Volume ComparisonProblems
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 1 / 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 156-169
- Print publication:
- 2013
-
- Article
- Export citation
Loss Reserves in the London Market
-
- Journal:
- British Actuarial Journal / Volume 1 / Issue 4 / 01 October 1995
- Published online by Cambridge University Press:
- 10 June 2011, pp. 689-760
-
- Article
- Export citation
Prospective Aging of the Population and Its Implications For the Labour Force and Government Expenditures
-
- Journal:
- Canadian Journal on Aging / La Revue canadienne du vieillissement / Volume 5 / Issue 2 / Summer/L'été 1986
- Published online by Cambridge University Press:
- 29 November 2010, pp. 75-98
-
- Article
- Export citation
Participation in Adult Education by the Elderly: A Multivariate Analysis and Some Implications for the Future
-
- Journal:
- Canadian Journal on Aging / La Revue canadienne du vieillissement / Volume 7 / Issue 1 / Spring/printemps 1988
- Published online by Cambridge University Press:
- 29 November 2010, pp. 4-16
-
- Article
- Export citation
Future costs of dementia-related long-term care: exploring future scenarios
-
- Journal:
- International Psychogeriatrics / Volume 23 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 08 April 2010, pp. 20-30
-
- Article
- Export citation