7 results
Limit theorems for continuous-state branching processes with immigration
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 599-624
- Print publication:
- June 2022
-
- Article
- Export citation
On strongly decreasing solutions of cyclic systems of second-order nonlinear differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 5 / October 2015
- Published online by Cambridge University Press:
- 02 September 2015, pp. 1007-1028
- Print publication:
- October 2015
-
- Article
- Export citation
General uniqueness results and variation speed for blow-up solutions of elliptic equations
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 91 / Issue 2 / September 2005
- Published online by Cambridge University Press:
- 23 August 2005, pp. 459-482
- Print publication:
- September 2005
-
- Article
- Export citation
Large deviations of tail estimators based on the Pareto approximation
-
- Journal:
- Journal of Applied Probability / Volume 24 / Issue 3 / September 1987
- Published online by Cambridge University Press:
- 14 July 2016, pp. 619-630
- Print publication:
- September 1987
-
- Article
- Export citation
Markov processes associated with critical Galton-Watson processes with application to extinction probabilities
-
- Journal:
- Advances in Applied Probability / Volume 8 / Issue 2 / June 1976
- Published online by Cambridge University Press:
- 01 July 2016, pp. 278-295
- Print publication:
- June 1976
-
- Article
- Export citation
On Zipf's law
-
- Journal:
- Journal of Applied Probability / Volume 12 / Issue 3 / September 1975
- Published online by Cambridge University Press:
- 14 July 2016, pp. 425-434
- Print publication:
- September 1975
-
- Article
- Export citation
Regularly varying functions in the theory of simple branching processes
-
- Journal:
- Advances in Applied Probability / Volume 6 / Issue 3 / September 1974
- Published online by Cambridge University Press:
- 01 July 2016, pp. 408-420
- Print publication:
- September 1974
-
- Article
- Export citation

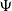
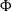
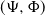
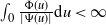
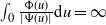
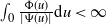
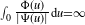
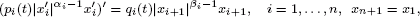
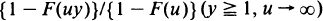 when this is approximated by
when this is approximated by 