The classical models in risk theory consider a single type of claim. In the insurance business, however, several business lines with separate claim arrival processes appear naturally, and the individual claim processes may not be independent. We introduce a new class of models for such situations, where the underlying counting process is a multivariate continuous-time Markov chain of pure-birth type and the dependency of the components arises from the fact that the birth rate for a specific claim type may depend on the number of claims in the other component processes. Under certain conditions, we obtain a fluid limit, i.e. a functional law of large numbers for these processes. We also investigate the consequences of such results for questions of interest in insurance applications. Several specific subclasses of the general model are discussed in detail and the Cramér asymptotics of the ruin probabilities are derived in particular cases.

The following problem in risk theory is considered. An insurance company, endowed with an initial capital a ≥ 0, receives premiums and pays out claims that occur according to a renewal process {N(t), t ≥ 0}. The times between consecutive claims are i.i.d. The sequence of successive claims is a sequence of i.i.d. random variables. The capital of the company is invested at interest rate α ∊ [0,1], claims increase at rate β ∊ [0,1]. The aim is to find the stopping time that maximizes the capital of the company. A dynamic programming method is used to find the optimal stopping time and to specify the expected capital at that time.

The risk reserve process of an insurance company within a deteriorating Markov-modulated environment is considered. The company invests its capital with interest rate α; the premiums and claims are increasing with rates β and γ. The problem of stopping the process at a random time which maximizes the expected net gain in order to calculate new premiums is investigated. A semimartingale representation of the risk reserve process yields, under certain conditions, an explicit solution of the problem.

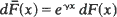Let Sn = X1 + · · · + Xn be a random walk with negative drift μ < 0, let F(x) = P(Xk ≦ x), v(u) =inf{n : Sn > u} and assume that for some γ > 0 is a proper distribution with finite mean 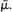Various limit theorems for functionals of 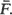X1,· · ·, Xv(u) are derived subject to conditioning upon {v(u)< ∞} with u large, showing similar behaviour as if the Xi were i.i.d. with distribution For example, the deviation of the empirical distribution function from 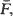properly normalised, is shown to have a limit in 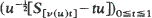D, and an approximation for by means of Brownian bridge is derived. Similar results hold for risk reserve processes in the time up to ruin and the 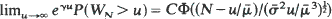GI/G/1 queue considered either within a busy cycle or in the steady state. The methods produce an alternate approach to known asymptotic formulae for ruin probabilities as well as related waiting-time approximations for the GI/G/1 queue. For example uniformly in N, with WN the waiting time of the Nth customer.