1 results
On population-size-dependent branching processes
-
- Journal:
- Advances in Applied Probability / Volume 16 / Issue 1 / March 1984
- Published online by Cambridge University Press:
- 01 July 2016, pp. 30-55
- Print publication:
- March 1984
-
- Article
- Export citation
-
We consider a stochastic model for the development in time of a population {Zn} where the law of offspring distribution depends on the population size. We are mainly concerned with the case when the mean mk and the variance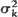
of offspring distribution stabilize as the population size k grows to ∞, 
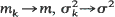The process exhibits different asymptotic behaviour according to m < l, m = 1, m> l; moreover, the rate of convergence of mk to m plays an important role. It is shown that if m < 1 or m = 1 and mn approaches 1 not slower than n–2 then the process dies out with probability 1. If mn approaches 1 from above and the rate of convergence is n–1, then Zn/n converges in distribution to a gamma distribution, moreover 
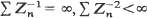a.s. both on a set of non-extinction and there are no constants an, such that Zn/an converges in probability to a non-degenerate limit. If mn approaches m > 1 not slower than n–α, α > 0, and 
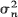do not grow to ∞ faster than nß, β <1 then Zn/mn converges almost surely and in L2 to a non-degenerate limit. A number of general results concerning the behaviour of sums of independent random variables are also given.
of offspring distribution stabilize as the population size 
The process exhibits different asymptotic behaviour according to m < l, 
a.s. both on a set of non-extinction and there are no constants 
do not grow to ∞ faster than 