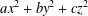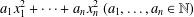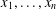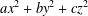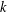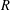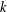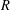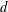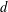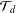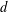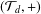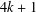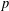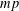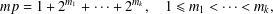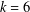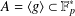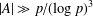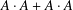5 results
PRIME-UNIVERSAL QUADRATIC FORMS
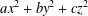 $ax^{2}+by^{2}+cz^{2}$ AND
$ax^{2}+by^{2}+cz^{2}$ AND  $ax^{2}+by^{2}+cz^{2}+dw^{2}$
$ax^{2}+by^{2}+cz^{2}+dw^{2}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 27 September 2019, pp. 1-12
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
FACTORS OF CARMICHAEL NUMBERS AND AN EVEN WEAKER
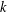 $k$-TUPLES CONJECTURE
$k$-TUPLES CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 20 February 2019, pp. 376-384
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
ALGEBRAIC AND GEOMETRIC PROPERTIES OF LATTICE WALKS WITH STEPS OF EQUAL LENGTH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 338-346
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
ALMOST ALL PRIMES HAVE A MULTIPLE OF SMALL HAMMING WEIGHT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 23 May 2016, pp. 224-235
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
WHEN THE SUM OF ALIQUOTS DIVIDES THE TOTIENT
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 50 / Issue 3 / October 2007
- Published online by Cambridge University Press:
- 08 January 2008, pp. 563-569
-
- Article
-
- You have access
- Export citation