Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
  1. Home
  2. Search

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

2 results

  • Rational points on linear slices of diagonal hypersurfaces

  • Part of
  • Jörg Brüdern, Olivier Robert
  • Journal:
    Nagoya Mathematical Journal / Volume 218 / June 2015
    Published online by Cambridge University Press:
    11 January 2016, pp. 51-100
    Print publication:
    June 2015
    • Article
      • You have access
    • PDF
    • Export citation

  • An asymptotic formula is obtained for the number of rational points of bounded height on the class of varieties described in the title line. The formula is proved via the Hardy-Littlewood method, and along the way we establish two new results on Weyl sums that are of some independent interest.

  • ON A DIAGONAL QUADRIC IN DENSE VARIABLES

  • EUGEN KEIL
  • Journal:
    Glasgow Mathematical Journal / Volume 56 / Issue 3 / September 2014
    Published online by Cambridge University Press:
    22 August 2014, pp. 601-628
    Print publication:
    September 2014
    • Article
      • You have access
    • PDF
    • Export citation

  • We examine the solubility of a diagonal, translation invariant, quadratic equation system in arbitrary (dense) subsets 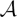$\mathcal{A}$ ⊂ ℤ and show quantitative bounds on the size of 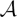$\mathcal{A}$ if there are no non-trivial solutions. We use the circle method and Roth's density increment argument. Due to a restriction theory approach we can deal with equations in s ≥ 7 variables.