23 results
First-order analysis of slip flow for micro and nanoscale applications
- Part of
-
- Journal:
- Flow: Applications of Fluid Mechanics / Volume 5 / 2025
- Published online by Cambridge University Press:
- 27 January 2025, E3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PHOTOFOCUSING OF MICROORGANISMS SWIMMING IN A FLOW WITH SHEAR
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 June 2018, pp. 455-471
-
- Article
-
- You have access
- Export citation
BIOLOGICAL FLUID MECHANICS UNDER THE MICROSCOPE: A TRIBUTE TO JOHN BLAKE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 416-442
-
- Article
-
- You have access
- Export citation
A Fifth-Order Combined Compact Difference Scheme for Stokes Flow on Polar Geometries
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 714-727
- Print publication:
- November 2017
-
- Article
- Export citation
FLUID FLOW AND PARTICLE TRANSPORT THROUGH PERIODIC CAPILLARIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 28 September 2017, pp. 521-522
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Stokes Flow of Viscous Fluid Past a Micropolar Fluid Spheroid
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 11 July 2017, pp. 1076-1093
- Print publication:
- October 2017
-
- Article
- Export citation
Numerical Computation of Doubly-Periodic Stokes Flow Bounded by a Plane with Applications to Nodal Cilia
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 06 July 2017, pp. 620-642
- Print publication:
- September 2017
-
- Article
- Export citation
EFFECTIVE SLIP LENGTH: SOME ANALYTICAL AND NUMERICAL RESULTS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 57 / Issue 1 / July 2015
- Published online by Cambridge University Press:
- 25 August 2015, pp. 79-88
-
- Article
-
- You have access
- Export citation
KELVIN–HELMHOLTZ CREEPING FLOW AT THE INTERFACE BETWEEN TWO VISCOUS FLUIDS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 02 July 2015, pp. 317-358
-
- Article
-
- You have access
- Export citation
Solution of Two-Dimensional Stokes Flow Problems Using Improved Singular Boundary Method
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 7 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 09 January 2015, pp. 13-30
- Print publication:
- February 2015
-
- Article
- Export citation
Exact Singularity Subtraction from Boundary Integral Equations in Modeling Vesicles and Red Blood Cells
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 7 / Issue 4 / November 2014
- Published online by Cambridge University Press:
- 09 August 2018, pp. 413-434
- Print publication:
- November 2014
-
- Article
- Export citation
Efficient Variable-Coefficient Finite-Volume Stokes Solvers
-
- Journal:
- Communications in Computational Physics / Volume 16 / Issue 5 / November 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 1263-1297
- Print publication:
- November 2014
-
- Article
- Export citation
Reduction of the Regularization Error of the Method of Regularized Stokeslets for a Rigid Object Immersed in a Three-Dimensional Stokes Flow
-
- Journal:
- Communications in Computational Physics / Volume 15 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 126-152
- Print publication:
- January 2014
-
- Article
- Export citation
A Hybrid Immersed Interface Method for Driven Stokes Flow in an Elastic Tube
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 6 / Issue 4 / November 2013
- Published online by Cambridge University Press:
- 28 May 2015, pp. 600-616-
- Print publication:
- November 2013
-
- Article
- Export citation
Steady symmetric low-Reynolds-number flow past a film-coated cylinder
-
- Journal:
- European Journal of Applied Mathematics / Volume 24 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 11 September 2012, pp. 1-24
-
- Article
- Export citation
Viscoelastic Immersed Boundary Methods for Zero Reynolds Number Flow
-
- Journal:
- Communications in Computational Physics / Volume 12 / Issue 2 / August 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 462-478
- Print publication:
- August 2012
-
- Article
- Export citation
CREEPING FLOW PAST A POROUS APPROXIMATELY SPHERICAL SHELL: STRESS JUMP BOUNDARY CONDITION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 3 / January 2011
- Published online by Cambridge University Press:
- 05 December 2011, pp. 289-300
-
- Article
-
- You have access
- Export citation
Numerical Study of Surfactant-Laden Drop-Drop Interactions
-
- Journal:
- Communications in Computational Physics / Volume 10 / Issue 2 / August 2011
- Published online by Cambridge University Press:
- 20 August 2015, pp. 453-473
- Print publication:
- August 2011
-
- Article
- Export citation
Microscopic Modelling of Active BacterialSuspensions
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 6 / Issue 5 / 2011
- Published online by Cambridge University Press:
- 10 August 2011, pp. 98-129
- Print publication:
- 2011
-
- Article
- Export citation
Slip velocity over a perforated or patchy surface
-
- Journal:
- Journal of Fluid Mechanics / Volume 643 / 25 January 2010
- Published online by Cambridge University Press:
- 15 January 2010, pp. 471-477
-
- Article
- Export citation

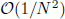 while the computational complexity is of order
while the computational complexity is of order 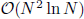 , where
, where 
