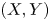16 results
Modeling of spatial extremes in environmental data science: time to move away from max-stable processes
-
- Journal:
- Environmental Data Science / Volume 4 / 2025
- Published online by Cambridge University Press:
- 15 January 2025, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extreme comovements and downside/upside risk spillovers between oil prices and exchange rates
-
- Journal:
- Macroeconomic Dynamics / Volume 29 / 2025
- Published online by Cambridge University Press:
- 05 November 2024, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measuring non-exchangeable tail dependence using tail copulas
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 28 February 2023, pp. 466-487
- Print publication:
- May 2023
-
- Article
- Export citation
Extreme Behaviors of the Tail Gini-Type Variability Measures
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 928-942
-
- Article
- Export citation
6 - Copulas
-
- Book:
- Quantitative Enterprise Risk Management
- Published online:
- 28 July 2022
- Print publication:
- 05 May 2022, pp 163-201
-
- Chapter
- Export citation
Bayesian vine copulas for modelling dependence in data breach losses
-
- Journal:
- Annals of Actuarial Science / Volume 16 / Issue 2 / July 2022
- Published online by Cambridge University Press:
- 03 February 2022, pp. 401-424
-
- Article
- Export citation
On the use of Archimedean copulas for insurance modelling
-
- Journal:
- Annals of Actuarial Science / Volume 15 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 June 2020, pp. 57-81
-
- Article
- Export citation
Simulation-based capital models: testing, justifying and communicating choices. A report from the life aggregation and simulation techniques working party
-
- Journal:
- British Actuarial Journal / Volume 22 / Issue 2 / July 2017
- Published online by Cambridge University Press:
- 17 April 2017, pp. 257-335
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PATHS AND INDICES OF MAXIMAL TAIL DEPENDENCE
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 45 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 19 June 2015, pp. 661-678
- Print publication:
- September 2015
-
- Article
- Export citation
COMPOSITE BERNSTEIN COPULAS
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 45 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 11 March 2015, pp. 445-475
- Print publication:
- May 2015
-
- Article
- Export citation
Relations Between Hidden Regular Variation and the Tail Order of Copulas
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 37-57
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
Diversification in heavy-tailed portfolios: properties and pitfalls
-
- Journal:
- Annals of Actuarial Science / Volume 7 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 19 November 2012, pp. 26-45
-
- Article
- Export citation
Extremal behavior of Archimedean copulas
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 195-216
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Tail Dependence for Heavy-Tailed Scale Mixtures of Multivariate Distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 925-937
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Limiting dependence structures for tail events, with applications to credit derivatives
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 563-586
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Multivariate extremes, aggregation and dependence in elliptical distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 3 / September 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 587-608
- Print publication:
- September 2002
-
- Article
- Export citation