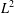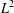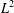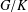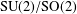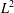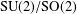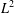18 results
THE WEYL TRANSFORM OF A SMOOTH MEASURE ON A REAL-ANALYTIC SUBMANIFOLD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1-10
-
- Article
-
- You have access
- HTML
- Export citation
On mixed fractional stochastic differential equations with discontinuous drift coefficient
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 01 December 2022, pp. 589-606
- Print publication:
- June 2023
-
- Article
- Export citation
3 - Some Calculus
- from PART I - Measure And Integration
-
- Book:
- Classical and Discrete Functional Analysis with Measure Theory
- Published online:
- 06 January 2022
- Print publication:
- 20 January 2022, pp 118-135
-
- Chapter
- Export citation
4 - Abstract Measures
- from PART I - Measure And Integration
-
- Book:
- Classical and Discrete Functional Analysis with Measure Theory
- Published online:
- 06 January 2022
- Print publication:
- 20 January 2022, pp 136-166
-
- Chapter
- Export citation
5 - Martingale Representations and Girsanov Transformations
- from Part I - Point Processes
-
- Book:
- Point Processes and Jump Diffusions
- Published online:
- 27 May 2021
- Print publication:
- 17 June 2021, pp 43-55
-
- Chapter
- Export citation
17 - Radon–Nikodým and Related Results
-
- Book:
- Counterexamples in Measure and Integration
- Published online:
- 27 May 2021
- Print publication:
- 17 June 2021, pp 317-329
-
- Chapter
- Export citation
Absolute continuity, Lyapunov exponents, and rigidity II: systems with compact center leaves
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 437-490
- Print publication:
- February 2022
-
- Article
- Export citation
On self-similar measures with absolutely continuous projections and dimension conservation in each direction
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 26 June 2019, pp. 3438-3456
- Print publication:
- December 2020
-
- Article
- Export citation
Compactness in quasi-Banach function spaces and applications to compact embeddings of Besov-type spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 23 June 2016, pp. 905-927
- Print publication:
- October 2016
-
- Article
- Export citation
SMOOTHNESS OF CONVOLUTION PRODUCTS OF ORBITAL MEASURES ON RANK ONE COMPACT SYMMETRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 12 February 2016, pp. 131-143
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
BOUNDS FOR THE DEVIATION OF A FUNCTION FROM THE CHORD GENERATED BY ITS EXTREMITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 225-248
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
A Full Descriptive Definition of the Henstock–Kurzweil Integral in the Euclidean Space
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 87 / Issue 3 / November 2003
- Published online by Cambridge University Press:
- 23 October 2003, pp. 677-700
- Print publication:
- November 2003
-
- Article
- Export citation
On fixed points of Poisson shot noise transforms
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 798-825
- Print publication:
- December 2002
-
- Article
- Export citation
ABSOLUTE CONTINUITY IN PERIODIC WAVEGUIDES
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 85 / Issue 3 / November 2002
- Published online by Cambridge University Press:
- 14 October 2002, pp. 717-741
- Print publication:
- November 2002
-
- Article
- Export citation
Robustness of the Ewens sampling formula
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 609-622
- Print publication:
- September 1995
-
- Article
- Export citation
A Characterization of Multi-Dimensional Perron Integrals and the Fundamental Theorem
-
- Journal:
- Canadian Journal of Mathematics / Volume 43 / Issue 3 / 01 June 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 526-539
- Print publication:
- 01 June 1991
-
- Article
-
- You have access
- Export citation
Continuity of limit random variables in the branching random walk
-
- Journal:
- Journal of Applied Probability / Volume 16 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 14 July 2016, pp. 740-749
- Print publication:
- December 1979
-
- Article
- Export citation
On supercritical Galton-Watson processes allowing immigration
-
- Journal:
- Journal of Applied Probability / Volume 11 / Issue 4 / December 1974
- Published online by Cambridge University Press:
- 14 July 2016, pp. 814-817
- Print publication:
- December 1974
-
- Article
- Export citation

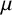
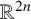
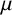


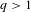
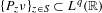

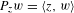
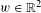

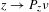
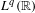
 , into Lorentz-type spaces.
, into Lorentz-type spaces.