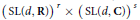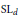1 results
Geometric Spectra and Commensurability
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 1 / 01 February 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 184-197
- Print publication:
- 01 February 2015
-
- Article
-
- You have access
- Export citation
-
The work of Reid, Chinburg–Hamilton–Long–Reid, Prasad–Rapinchuk, and the author with Reid have demonstrated that geodesics or totally geodesic submanifolds can sometimes be used to determine the commensurability class of an arithmetic manifold. The main results of this article show that generalizations of these results to other arithmetic manifolds will require a wide range of data. Specifically, we prove that certain incommensurable arithmetic manifolds arising from the semisimple Lie groups of the form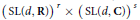
${{\left( \text{SL(d,}\,\mathbf{R}) \right)}^{r}}\,\times \,{{\left( \text{SL(d,}\,\mathbf{C}) \right)}^{s}}$ have the same commensurability classes of totally geodesic submanifolds coming from a fixed field. This construction is algebraic and shows the failure of determining, in general, a central simple algebra from subalgebras over a fixed field. This, in turn, can be viewed in terms of forms of 
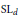$\text{S}{{\text{L}}_{d}}$ and the failure of determining the form via certain classes of algebraic subgroups.
