1 results
Fixed Point Theorems for Proximately Nonexpansive Semigroups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 29 / Issue 2 / 01 June 1986
- Published online by Cambridge University Press:
- 20 November 2018, pp. 160-166
- Print publication:
- 01 June 1986
-
- Article
-
- You have access
- Export citation
-
A commutative semigroup G of continuous, selfmappings on (X, d) is called proximately nonexpansive on X if for every x in X and every (β > 0, there is a member g in G such that d(fg(x),fg(y)) ≤ (1 + β) d (x, y) for every f in G and y in X. For a uniformly convex Banach space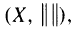
it is shown that if G is a commutative semigroup of continuous selfmappings on X which is proximately nonexpansive, then a common fixed point exists if there is an x0 in X such that its orbit G(x0) is bounded. Furthermore, the asymptotic center of G(x0) is such a common fixed point.
it is shown that if G is a commutative semigroup of continuous selfmappings on X which is proximately nonexpansive, then a common fixed point exists if there is an x