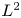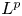25 results
OPTIMAL QUEUING STRATEGIES FOR AN M/G/1 RETRIAL QUEUE SYSTEM WITH RWV AND ISEV POLICIES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 19 March 2024, pp. 384-410
-
- Article
-
- You have access
- HTML
- Export citation
Stability properties of multidimensional symmetric hyperbolic systems with damping, differential constraints and delay
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 September 2023, pp. 1-43
-
- Article
- Export citation
On stability for generalized linear differential equations and applications to impulsive systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 February 2023, pp. 381-407
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
4 - Asymptotic Stability of Stationary Orbits and Solitons
-
- Book:
- Attractors of Hamiltonian Nonlinear Partial Differential Equations
- Published online:
- 17 September 2021
- Print publication:
- 30 September 2021, pp 114-165
-
- Chapter
- Export citation
Asymptotic stability of rarefaction wave for the compressible Navier‐Stokes‐Korteweg equations in the half space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 23 July 2021, pp. 756-779
- Print publication:
- June 2022
-
- Article
- Export citation
Hilbert–Mumford criterion for nodal curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 10 June 2015, pp. 2076-2130
- Print publication:
- November 2015
-
- Article
- Export citation
A new stabilizing solution for motion planning and control of multiple robots
-
- Article
-
- You have access
- Open access
- Export citation
Asymptotic Stability of an Eikonal Transformation Based ADI Method for the Paraxial Helmholtz Equation at High Wave Numbers
-
- Journal:
- Communications in Computational Physics / Volume 12 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 1275-1292
- Print publication:
- October 2012
-
- Article
- Export citation
REPLICATOR DYNAMIC LEARNING IN MUTH'S MODEL OF PRICE MOVEMENTS
-
- Journal:
- Macroeconomic Dynamics / Volume 18 / Issue 3 / April 2014
- Published online by Cambridge University Press:
- 13 September 2012, pp. 573-592
-
- Article
- Export citation
Controller design for bush-type 1-d wave networks∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 02 December 2010, pp. 208-228
- Print publication:
- January 2012
-
- Article
- Export citation
Switching and stability propertiesof conewise linear systems
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 16 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 02 July 2009, pp. 764-793
- Print publication:
- July 2010
-
- Article
- Export citation
Stability analysis of a k-out-of-N:G reparable system
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 271-284
-
- Article
-
- You have access
- Export citation
Direct design of robustly asymptotically stabilizing hybrid feedback
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 15 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 23 January 2009, pp. 205-213
- Print publication:
- January 2009
-
- Article
- Export citation
Asymptotic stability of linear conservative systemswhen coupledwith diffusive systems
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 11 / Issue 3 / July 2005
- Published online by Cambridge University Press:
- 15 July 2005, pp. 487-507
- Print publication:
- July 2005
-
- Article
- Export citation